Diferencia entre revisiones de «Red de Petri»
(→Red de Petri marcada) |
|||
| (No se muestran 2 ediciones intermedias de 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | |||
{{Definición | {{Definición | ||
|nombre= Red de Petri | |nombre= Red de Petri | ||
|imagen= | |imagen= | ||
|tamaño= | |tamaño= | ||
| − | |concepto=Una [[red de Petri]] es una [[gráfica]] dirigida G=(V,E) donde V= P U T y P ∩ T = Ø . Cualquier arista e en E es incidente en un miembro de P y un miembro de T. El conjunto P es el conjunto de los <i>lugares</i> y el conjunto T es el conjunto de <i> transiciones</i>. De manera informal, una red de Petri es una gráfica dirigida, | + | |concepto=Una [[red de Petri]] es una [[gráfica]] dirigida G= (V,E) donde V= P U T y P ∩ T = Ø . Cualquier arista e en E es incidente en un miembro de P y un miembro de T. El conjunto P es el conjunto de los <i>lugares</i> y el conjunto T es el conjunto de <i> transiciones</i>. De manera informal, una red de Petri es una gráfica dirigida, bipartita, en la cual las dos clases de vértices se llaman lugares y transiciones. En general en las redes de Petri se permite la existencia de aristas paralelas. <br/> |
}} | }} | ||
'''Redes de Petri''' | '''Redes de Petri''' | ||
| − | + | ||
==Explicación== | ==Explicación== | ||
| − | Consideremos el siguiente fragmento de código de un [[programa de computadoras]]:<br/> | + | Consideremos el siguiente fragmento de código de un [[programa de computadoras]]: <br/> |
<b> A = 1<br/> | <b> A = 1<br/> | ||
B = 2 <br/> | B = 2 <br/> | ||
| Línea 16: | Línea 15: | ||
C = B + C <br/> | C = B + C <br/> | ||
B = A + C <br/></b> | B = A + C <br/></b> | ||
| − | En general las instrucciones se procesarían en forma secuencial, sin embargo no existe una razón lógica para evitar que las tres primeras instrucciones se procesen en un orden arbitrario o de manera concurrente. Al disminuir los costos del [[hardware]] y de los [[procesadores]] en particular existe un creciente interés en el procesamiento concurrente, para lograr una mayor velocidad y eficiencia. El uso de <b> redes de Petri</b> es un método para estudiar el procesamiento concurrente.<br/> | + | En general las instrucciones se procesarían en forma secuencial, sin embargo no existe una razón lógica para evitar que las tres primeras instrucciones se procesen en un orden arbitrario o de manera concurrente. Al disminuir los costos del [[hardware]] y de los [[Microprocesadores|procesadores]] en particular existe un creciente interés en el procesamiento concurrente, para lograr una mayor velocidad y eficiencia. El uso de <b> redes de Petri</b> es un método para estudiar el procesamiento concurrente. <br/> |
| − | En general en una red de Petri (como se muestra en la figura anterior), los lugares se dibujan como círculos y las transiciones como barras o cajas rectangulares.<br/> | + | En general en una red de Petri (como se muestra en la figura anterior), los lugares se dibujan como círculos y las transiciones como barras o cajas rectangulares. <br/> |
[[archivo:Petri1.JPG|thumbs|center|Red de Petri]] | [[archivo:Petri1.JPG|thumbs|center|Red de Petri]] | ||
| + | |||
== Red de Petri marcada == | == Red de Petri marcada == | ||
| − | Un <i> marcado </i> de una red de Petri asigna a cada lugar un entero no negativo. Una red de Petri con un marcado es una <i> Red de Petri Marcada </i> o simplemente una red de Petri.<br/> | + | Un <i> marcado </i> de una red de Petri asigna a cada lugar un entero no negativo. Una red de Petri con un marcado es una <i> Red de Petri Marcada </i> o simplemente una red de Petri. <br/> |
[[archivo:Petri2.JPG|thumbs|center|Red de Petri marcada]] | [[archivo:Petri2.JPG|thumbs|center|Red de Petri marcada]] | ||
| − | Si un marcado asigna el entero no negativo n al lugar p, decimos que existen n elementos en p. Los elementos se representan mediante puntos.<br/> | + | Si un marcado asigna el entero no negativo n al lugar p, decimos que existen n elementos en p. Los elementos se representan mediante puntos. <br/> |
| − | Al modelar una situación, los lugares representan <b>condiciones</b>, las transiciones representan <b>eventos</b>, y la presencia de al menos un elemento en un lugar indica que tal condición se cumple.<br/> | + | Al modelar una situación, los lugares representan <b>condiciones</b>, las transiciones representan <b>eventos</b>, y la presencia de al menos un elemento en un lugar indica que tal condición se cumple. <br/> |
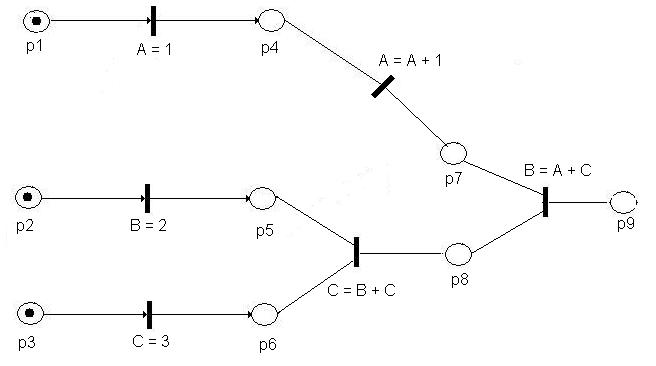
| − | Utilizando estos conceptos el fragmento de código del inicio puede ser modelado mediante una red de Petri | + | Utilizando estos conceptos el fragmento de código del inicio puede ser modelado mediante una red de Petri tal y como se muestra en la siguiente figura. <br/> |
[[archivo:Petri3.JPG|thumbs|center|Red de Petri modelada]] | [[archivo:Petri3.JPG|thumbs|center|Red de Petri modelada]] | ||
En una red de Petri, si una arista va de un lugar p a una transición t, decimos que p es un lugar de entrada para la transición t. Un lugar de salida se define de manera análoga. Si cada lugar de entrada de una transición t tiene al menos un elemento decimos que t está activada. La descarga de la transición t elimina un elemento de cada lugar de entrada y agrega un elemento a cada lugar de salida. | En una red de Petri, si una arista va de un lugar p a una transición t, decimos que p es un lugar de entrada para la transición t. Un lugar de salida se define de manera análoga. Si cada lugar de entrada de una transición t tiene al menos un elemento decimos que t está activada. La descarga de la transición t elimina un elemento de cada lugar de entrada y agrega un elemento a cada lugar de salida. | ||
| + | |||
| + | ==Fuentes== | ||
| − | + | * Johnsonbaugh, Richard. Matemáticas Discretas. Volumen II, cuarta edición. Editorial Felix Varela, La Habana, 2006. Pág 486 | |
| − | |||
| − | * Johnsonbaugh, Richard. Matemáticas Discretas. Volumen II,cuarta edición.Editorial Felix Varela, La | ||
* Información ofrecida por MSc. José Ramón Ávila Cruz. [[Joven Club Puerto Padre V]]. | * Información ofrecida por MSc. José Ramón Ávila Cruz. [[Joven Club Puerto Padre V]]. | ||
[[Categoría: Matemáticas]] | [[Categoría: Matemáticas]] | ||
última versión al 10:24 12 jun 2012
| ||||
Redes de Petri
Explicación
Consideremos el siguiente fragmento de código de un programa de computadoras:
A = 1
B = 2
C = 3
A = A + 1
C = B + C
B = A + C
En general las instrucciones se procesarían en forma secuencial, sin embargo no existe una razón lógica para evitar que las tres primeras instrucciones se procesen en un orden arbitrario o de manera concurrente. Al disminuir los costos del hardware y de los procesadores en particular existe un creciente interés en el procesamiento concurrente, para lograr una mayor velocidad y eficiencia. El uso de redes de Petri es un método para estudiar el procesamiento concurrente.
En general en una red de Petri (como se muestra en la figura anterior), los lugares se dibujan como círculos y las transiciones como barras o cajas rectangulares.
Red de Petri marcada
Un marcado de una red de Petri asigna a cada lugar un entero no negativo. Una red de Petri con un marcado es una Red de Petri Marcada o simplemente una red de Petri.
Si un marcado asigna el entero no negativo n al lugar p, decimos que existen n elementos en p. Los elementos se representan mediante puntos.
Al modelar una situación, los lugares representan condiciones, las transiciones representan eventos, y la presencia de al menos un elemento en un lugar indica que tal condición se cumple.
Utilizando estos conceptos el fragmento de código del inicio puede ser modelado mediante una red de Petri tal y como se muestra en la siguiente figura.
En una red de Petri, si una arista va de un lugar p a una transición t, decimos que p es un lugar de entrada para la transición t. Un lugar de salida se define de manera análoga. Si cada lugar de entrada de una transición t tiene al menos un elemento decimos que t está activada. La descarga de la transición t elimina un elemento de cada lugar de entrada y agrega un elemento a cada lugar de salida.
Fuentes
- Johnsonbaugh, Richard. Matemáticas Discretas. Volumen II, cuarta edición. Editorial Felix Varela, La Habana, 2006. Pág 486
- Información ofrecida por MSc. José Ramón Ávila Cruz. Joven Club Puerto Padre V.