Diferencia entre revisiones de «Tautología»
(Página creada con '{{Definición |nombre=tautologías |imagen= |tamaño= |concepto= tautologías }} =='''Tautologías'''== Una proposición compuesta es una tautología si es verdadera, cual...') |
|||
| (No se muestran 2 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
{{Definición | {{Definición | ||
| − | |nombre= | + | |nombre=Tautologías |
| − | |imagen= | + | |imagen= Tautologia.png |
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto= Es una expresión lógica que resulta verdadera para cualquier interpretación |
| − | }} | + | }}<div align="justify">'''Tautologías'''. Una proposición compuesta es una tautología si es verdadera, cualesquiera que sean los valores de verdad de las proposiciones simples que la componen. |
| − | |||
| − | |||
| − | Una proposición compuesta es una tautología si es verdadera, cualesquiera que sean los valores de | ||
| − | verdad de las proposiciones simples que la componen. | ||
En una tautología se pueden sustituir sus proposiciones simples por otras proposiciones simples | En una tautología se pueden sustituir sus proposiciones simples por otras proposiciones simples | ||
cualesquiera verdaderas o falsas y la proposición también es verdadera. | cualesquiera verdaderas o falsas y la proposición también es verdadera. | ||
| Línea 15: | Línea 11: | ||
==¿Es la proposición p∨q→p una tautología?== | ==¿Es la proposición p∨q→p una tautología?== | ||
| − | '''Definición:''' Una [[proposición]] es una tautología si y solo si es verdadera para todas las combinaciones de asignaciones de valores de verdad atribuidas a cada una de las distintas | + | '''Definición:''' Una [[proposición]] es una tautología si y solo si es verdadera para todas las combinaciones de asignaciones de valores de verdad atribuidas a cada una de las distintas |
| − | proposiciones simples. Una proposición p implica tautológicamente una proposición q | + | proposiciones simples. Una proposición p implica tautológicamente una proposición q si y solo si el condicional p→q es una tautología. Así, una implicación tautológica es una |
| − | si y solo si el condicional p→q es una | + | tautología cuya forma es la de una proposición condicional. Una proposición que es una implicación tautológica indica que el condicional correspondiente es una tautología. Para verificar si una proposición compuesta es una tautología se hace uso del método de la tabla de verdad. |
| − | tautología cuya forma es la de una proposición condicional. Una proposición que es una implicación tautológica indica que el condicional correspondiente es una tautología. Para verificar si una proposición | ||
| − | compuesta es una tautología se hace uso del método de | ||
==Ejercicios== | ==Ejercicios== | ||
| Línea 39: | Línea 33: | ||
Una contradicción es una proposición simbolizada que es falsa en todos los casos (es decir, | Una contradicción es una proposición simbolizada que es falsa en todos los casos (es decir, | ||
| − | independientemente del valor de verdad de las proposiciones simples que la compongan y de cuáles se tales proposiciones simples). En este sentido las contradicciones son exactamente lo opuesto de las | + | independientemente del valor de verdad de las proposiciones simples que la compongan y de cuáles se tales proposiciones simples). En este sentido las contradicciones son exactamente lo opuesto de las tautologías: son las ―antileyes de la lógica. |
| − | tautologías: son las ―antileyes de la lógica. | + | |
| − | |||
| − | |||
| − | |||
==Enlaces externos== | ==Enlaces externos== | ||
* http://yrosero.jimdo.com/curso-logica-matematica-programa-de-fisioterapia/ | * http://yrosero.jimdo.com/curso-logica-matematica-programa-de-fisioterapia/ | ||
[[Category:Ciencias_Aplicadas_y_Tecnologías]] | [[Category:Ciencias_Aplicadas_y_Tecnologías]] | ||
última versión al 14:08 16 sep 2013
| ||||||
En una tautología se pueden sustituir sus proposiciones simples por otras proposiciones simples cualesquiera verdaderas o falsas y la proposición también es verdadera. Por ejemplo para cualesquier proposición simple p , p∨∽p es una tautología
¿Es la proposición p∨q→p una tautología?
Definición: Una proposición es una tautología si y solo si es verdadera para todas las combinaciones de asignaciones de valores de verdad atribuidas a cada una de las distintas proposiciones simples. Una proposición p implica tautológicamente una proposición q si y solo si el condicional p→q es una tautología. Así, una implicación tautológica es una tautología cuya forma es la de una proposición condicional. Una proposición que es una implicación tautológica indica que el condicional correspondiente es una tautología. Para verificar si una proposición compuesta es una tautología se hace uso del método de la tabla de verdad.
Ejercicios
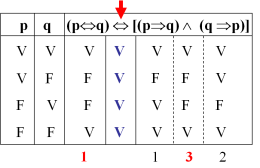
Si p y q son proposiciones simples diferentes, determine cuáles de las siguientes proposiciones son tautologías? (p→q)↔(q→p) (~p∨∼q)→(p→q) (p→q)↔∼(p∧∼q ∼(p∧∼q)↔ ~p∨q) p→~p Sean P,Q y R proposiciones simples diferentes, determine cuáles de las proposiciones siguientes son tautologías? P→P∨Q∨R P∧Q→P∨R
Definición
Se dice que dos proposiciones son lógicamente equivalentes si en cualquier posible asignación de valor de verdad las dos tienen el mismo.
Una contradicción es una proposición simbolizada que es falsa en todos los casos (es decir, independientemente del valor de verdad de las proposiciones simples que la compongan y de cuáles se tales proposiciones simples). En este sentido las contradicciones son exactamente lo opuesto de las tautologías: son las ―antileyes de la lógica.