Diferencia entre revisiones de «Sistema de fuerzas concurrentes»
(Página creada con '{{Desarrollo}}{{Definición |nombre= Sistema de fuerzas concurrentes |imagen= |tamaño= |concepto= Capacidad de hacer o actuar sobre algo.}} <div align="justify"> '''Sistema de ...') |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 7 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
| − | + | {{Definición | |
|nombre= Sistema de fuerzas concurrentes | |nombre= Sistema de fuerzas concurrentes | ||
|imagen= | |imagen= | ||
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto= [[Fuerza]]s cuyas líneas de acción se intersecan en un punto.}} |
| − | + | ||
| − | '''Sistema de fuerzas concurrentes'''. Sistema de fuerzas perteneciente a la [[Estática|estática]]. | + | '''Sistema de fuerzas concurrentes'''. Sistema de fuerzas perteneciente a la [[Estática|estática]]. Se presentan ejemplos concretos sobre el comportamiento de dichas fuerzas. |
==Definición== | ==Definición== | ||
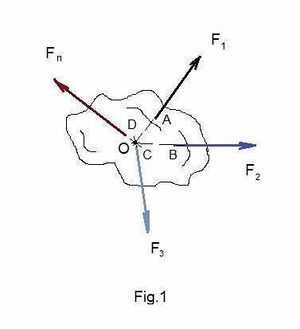
| − | Se conoce como sistema de fuerzas concurrentes a las fuerzas cuyas líneas de acción se intersecan en un punto (Nikitín, [[1980]], p.35). Si se trasladan todas las fuerzas del sistema dado por sus líneas de acción al punto común de intersección de estas líneas, el punto O, entonces, según el principio de la transmisibilidad, la acción del sistema sobre un cuerpo rígido no cambiará. Por lo tanto, cualquier sistema de fuerzas concurrentes puede ser sustituido por un sistema de fuerzas equivalente aplicadas a un mismo punto. Son coplanares cuando se encuentran en un mismo plano. (Fig.1) | + | Se conoce como sistema de fuerzas concurrentes a las fuerzas cuyas líneas de acción se intersecan en un punto (Nikitín, [[1980]], p.35). Si se trasladan todas las fuerzas del sistema dado por sus líneas de acción al punto común de intersección de estas líneas, el punto '''O''', entonces, según el principio de la transmisibilidad, la acción del sistema sobre un cuerpo rígido no cambiará. Por lo tanto, cualquier sistema de fuerzas concurrentes puede ser sustituido por un sistema de fuerzas equivalente aplicadas a un mismo punto. Son coplanares cuando se encuentran en un mismo plano. (Fig.1) |
| − | + | [[Image:Fuerzas_c_Fig-1.jpg|thumb|center]] | |
| + | |||
==Composición de fuerzas concurrentes== | ==Composición de fuerzas concurrentes== | ||
La composición de fuerzas concurrentes tiene por objeto, dado un sistema de [[fuerza]]s hallar su resultante. | La composición de fuerzas concurrentes tiene por objeto, dado un sistema de [[fuerza]]s hallar su resultante. | ||
| − | El problema de la composición de dos fuerzas aplicadas a un mismo punto se soluciona de manera simple, si se aplica el principio del paralelogramo de fuerzas, o construyendo el triángulo de fuerzas que representa una mitad de este paralelogramo. Supóngase que al punto O de un cuerpo sólido se han aplicado dos fuerzas F1 y F2 (Fig.2a), la resultante R de las fuerzas dadas está aplicada al mismo punto O y se representa en módulo y dirección por la diagonal OC del paralelogramo construido con dichas fuerzas tomadas como lados (Fig. 2b). | + | |
| − | Se define como escala de fuerza, al número que representa o indica cuántos néwtones (N) de fuerza real corresponde a un milímetro de vector fuerza en el dibujo. | + | El problema de la composición de dos fuerzas aplicadas a un mismo punto se soluciona de manera simple, si se aplica el principio del [[paralelogramo]] de fuerzas, o construyendo el [[triángulo]] de fuerzas que representa una mitad de este paralelogramo. Supóngase que al punto '''O''' de un cuerpo sólido se han aplicado dos fuerzas '''F1''' y '''F2''' (Fig.2a), la resultante '''R''' de las fuerzas dadas está aplicada al mismo punto '''O''' y se representa en módulo y dirección por la diagonal '''OC''' del paralelogramo construido con dichas fuerzas tomadas como lados (Fig. 2b). |
| − | + | ||
| + | Se define como escala de fuerza, al número que representa o indica cuántos néwtones ('''N''') de fuerza real corresponde a un milímetro de vector fuerza en el dibujo. | ||
| + | |||
| + | µf = F1/OA = N/mm | ||
| + | |||
De donde R = OC µf | De donde R = OC µf | ||
| − | Para determinar la resultante no hay necesidad de construir todo el | + | |
| + | Para determinar la resultante no hay necesidad de construir todo el paralelogramo '''AOBC''', basta construir solamente uno de los triángulos '''OAC''' ó '''OBC'''. Construyamos uno de estos triángulos, el '''OBC''' (Fig.2c). Para esto, a partir de un punto arbitrario '''A1''', trazamos el vector '''A1B''', que representa la fuerza '''F2''', desde el extremo de este vector, trazamos el vector '''BC''', igual al vector '''F1'''. El lado '''A1C''' que cierra el triángulo '''A1BC''' representa el módulo y dirección de la resultante de las dos fuerzas concurrentes. Queda sólo medir, en la escala adoptada, su longitud. | ||
| + | |||
Conforme al teorema de los cosenos | Conforme al teorema de los cosenos | ||
| + | |||
R2 = F12 + F22 – 2 F1 F2 cos(1800 – α) | R2 = F12 + F22 – 2 F1 F2 cos(1800 – α) | ||
Como cos(1800 – α) = - cosα se obtiene | Como cos(1800 – α) = - cosα se obtiene | ||
| − | + | _____________________ | |
| − | + | ||
| + | R = \̸ F12 + F22 + 2 F1 F2 cosα | ||
Si el ángulo entre las fuerzas dadas es α = 900, entonces | Si el ángulo entre las fuerzas dadas es α = 900, entonces | ||
| − | + | ||
| + | cos α = cos 900 = 0 | ||
| + | |||
Y el módulo de la resultante. | Y el módulo de la resultante. | ||
| − | + | ________ | |
| − | + | ||
| − | + | R = √ F12 + F22 | |
| − | La dirección de la resultante se establece según el teorema de los senos, | + | [[Image:Fuerzas c Fig-2.jpg|thumb|center|Módulo resultante]] |
| − | + | La dirección de la resultante se establece según el teorema de los senos, "en todo triángulo los lados son proporcionales a los senos de los ángulos opuestos por el vértice". Al mismo tiempo "los lados del triángulo son proporcionales a los módulos de las fuerzas". De donde se obtiene: | |
| − | + | ||
| − | + | F1 F2 R | |
| + | |||
| + | --------- = --------- = --------- | ||
| + | |||
| + | sen β sen φ sen α | ||
| + | |||
==Composición de varias fuerzas concurrentes== | ==Composición de varias fuerzas concurrentes== | ||
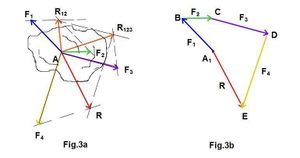
| − | La composición de varias fuerzas aplicadas | + | La composición de varias fuerzas aplicadas en un punto puede ser efectuada mediante el empleo sucesivo del principio del paralelogramo de fuerzas o mediante la regla del polígono de fuerzas. Utilizando la regla o principio del paralelogramo, primeramente se componen las fuerzas '''F1''' y '''F2''' y se halla su resultante '''R12'''. Esta debe componerse con la fuerza '''F3''', hallando la resultante '''R123''' y así sucesivamente hasta obtener la resultante final '''R''' (Fig.3a). |
| − | La resultante de las fuerzas se puede obtener mediante la regla del polígono de fuerzas. Para esto, a partir de un punto arbitrario A1(Fig.3b), | + | |
| − | + | La resultante de las fuerzas se puede obtener mediante la regla del [[polígono]] de fuerzas. Para esto, a partir de un punto arbitrario '''A1'''(Fig.3b), trazando el vector '''A1B''' que representa la fuerza '''F1''' en la escala elegida, desde el punto '''B''', se traza el vector '''BC''', que representa la fuerza '''F2''', así sucesivamente, hasta unir el origen del primer vector con el extremo de la última fuerza, el vector '''R''', representa la resultante del sistema de fuerzas concurrentes. Es fácil comprender que la construcción hecha representa el resultado de la aplicación consecutiva de la regla del triángulo de fuerzas. | |
| − | El contorno A1BCDE obtenido constituye un polígono, cuyos lados representa todas las fuerzas que actúan en un punto (polígono de fuerzas). | + | [[Image:Fuerzas_c_Fig-3.jpg|thumb|center]] |
| + | El contorno '''A1BCDE''' obtenido constituye un polígono, cuyos lados representa todas las fuerzas que actúan en un punto (polígono de fuerzas). | ||
| + | |||
==Descomposición de una fuerza en componentes== | ==Descomposición de una fuerza en componentes== | ||
| − | La descomposición de una fuerza en componentes, significa hallar unas fuerzas tales que estando aplicadas en un mismo punto, efectúan una acción equivalente a la fuerza que se descompone. Con otras palabras, descomponer una fuerza, en componentes, significa hallar tal sistema de fuerzas, que produzca el mismo efecto que la fuerza dada (Ballester, 1995, p.26). | + | La descomposición de una [[fuerza]] en componentes, significa hallar unas fuerzas tales que estando aplicadas en un mismo punto, efectúan una acción equivalente a la fuerza que se descompone. Con otras palabras, descomponer una fuerza, en componentes, significa hallar tal sistema de fuerzas, que produzca el mismo efecto que la fuerza dada (Ballester, [[1995]], p.26). |
| + | |||
La descomposición de una fuerza dada en dos componentes coplanares, por lo general es un problema indeterminado, es necesario estipular algunas condiciones, para que la solución sea determinada: | La descomposición de una fuerza dada en dos componentes coplanares, por lo general es un problema indeterminado, es necesario estipular algunas condiciones, para que la solución sea determinada: | ||
| − | + | #La fijación de dos direcciones, en las cuales deben obrar las componentes. | |
| − | + | #La fijación del módulo y dirección de una de las fuerzas componentes. | |
| − | + | #La fijación de los módulos de las dos fuerzas componentes. | |
| − | + | #La fijación del módulo de una fuerza componente y la dirección de la otra. | |
| − | + | ||
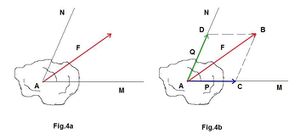
| − | + | Analícese el primer caso, que es el que aparece con mayor frecuencia: Se necesita descomponer la fuerza '''F''' en dos fuerzas, las direcciones de las cuales están dadas '''AM''' y '''AN''' (Fig.4a). El problema se resuelve, trazando desde el extremo de la fuerza '''F''' las rectas '''BC''' y '''BD''' paralelas a las rectas '''AM''' y '''AN''' respectivamente. Los vectores '''AC''' y '''AD''' proporcionan, en la misma escala que la fuerza '''F''', las componentes '''P''' y '''Q''' que se buscan (Fig.4b). | |
| + | [[Image:Fuerzas_c_Fig-4.jpg|thumb|center]] | ||
| + | |||
==Fuentes== | ==Fuentes== | ||
| − | Ballester Gouraige, Andrés. Fundamentos de Mecánica Teórica y Teoría de los Mecanismos. Editado Departamento E.T.P | + | #Ballester Gouraige, Andrés. Fundamentos de Mecánica Teórica y Teoría de los Mecanismos. Editado Departamento E.T.P, [[Universidad de Ciencias Pedagógicas "Raúl Gómez García"|I.S.P. "Raúl Gómez García"]], [[Guantánamo]]. [[1995]]. |
| − | Nikitin, E.M. Mecánica Teórica para las escuelas de peritaje. Ed. MIR, Moscú, 1980. | + | #Nikitin, E.M. Mecánica Teórica para las escuelas de peritaje. [[Editorial MIR|Ed. MIR]], [[Moscú]], [[1980]]. |
| − | Sokolov, F y P. Usov. Mecánica Industrial. Tercera edición. Ed. MIR, Moscú, 1986. | + | #Sokolov, F y P. Usov. Mecánica Industrial. Tercera edición. Ed. MIR, Moscú, [[1986]]. |
| − | Starzhinski, V.M. Mecánica Teórica. Ed. MIR, Moscú, 1980. | + | #Starzhinski, V.M. [[Mecánica Teórica]]. Ed. MIR, Moscú, 1980. |
| − | Targ, S.M. Curso breve de Mecánica Teórica. Cuarta edición. Ed. MIR, Moscú, 1976. | + | #Targ, S.M. Curso breve de Mecánica Teórica. Cuarta edición. Ed. MIR, Moscú, [[1976]]. |
[[Category:Mecánica]] | [[Category:Mecánica]] | ||
última versión al 07:29 3 sep 2019
| ||||
Sistema de fuerzas concurrentes. Sistema de fuerzas perteneciente a la estática. Se presentan ejemplos concretos sobre el comportamiento de dichas fuerzas.
Sumario
Definición
Se conoce como sistema de fuerzas concurrentes a las fuerzas cuyas líneas de acción se intersecan en un punto (Nikitín, 1980, p.35). Si se trasladan todas las fuerzas del sistema dado por sus líneas de acción al punto común de intersección de estas líneas, el punto O, entonces, según el principio de la transmisibilidad, la acción del sistema sobre un cuerpo rígido no cambiará. Por lo tanto, cualquier sistema de fuerzas concurrentes puede ser sustituido por un sistema de fuerzas equivalente aplicadas a un mismo punto. Son coplanares cuando se encuentran en un mismo plano. (Fig.1)
Composición de fuerzas concurrentes
La composición de fuerzas concurrentes tiene por objeto, dado un sistema de fuerzas hallar su resultante.
El problema de la composición de dos fuerzas aplicadas a un mismo punto se soluciona de manera simple, si se aplica el principio del paralelogramo de fuerzas, o construyendo el triángulo de fuerzas que representa una mitad de este paralelogramo. Supóngase que al punto O de un cuerpo sólido se han aplicado dos fuerzas F1 y F2 (Fig.2a), la resultante R de las fuerzas dadas está aplicada al mismo punto O y se representa en módulo y dirección por la diagonal OC del paralelogramo construido con dichas fuerzas tomadas como lados (Fig. 2b).
Se define como escala de fuerza, al número que representa o indica cuántos néwtones (N) de fuerza real corresponde a un milímetro de vector fuerza en el dibujo.
µf = F1/OA = N/mm
De donde R = OC µf
Para determinar la resultante no hay necesidad de construir todo el paralelogramo AOBC, basta construir solamente uno de los triángulos OAC ó OBC. Construyamos uno de estos triángulos, el OBC (Fig.2c). Para esto, a partir de un punto arbitrario A1, trazamos el vector A1B, que representa la fuerza F2, desde el extremo de este vector, trazamos el vector BC, igual al vector F1. El lado A1C que cierra el triángulo A1BC representa el módulo y dirección de la resultante de las dos fuerzas concurrentes. Queda sólo medir, en la escala adoptada, su longitud.
Conforme al teorema de los cosenos
R2 = F12 + F22 – 2 F1 F2 cos(1800 – α) Como cos(1800 – α) = - cosα se obtiene _____________________
R = \̸ F12 + F22 + 2 F1 F2 cosα
Si el ángulo entre las fuerzas dadas es α = 900, entonces
cos α = cos 900 = 0
Y el módulo de la resultante. ________
R = √ F12 + F22
La dirección de la resultante se establece según el teorema de los senos, "en todo triángulo los lados son proporcionales a los senos de los ángulos opuestos por el vértice". Al mismo tiempo "los lados del triángulo son proporcionales a los módulos de las fuerzas". De donde se obtiene:
F1 F2 R
= --------- = ---------
sen β sen φ sen α
Composición de varias fuerzas concurrentes
La composición de varias fuerzas aplicadas en un punto puede ser efectuada mediante el empleo sucesivo del principio del paralelogramo de fuerzas o mediante la regla del polígono de fuerzas. Utilizando la regla o principio del paralelogramo, primeramente se componen las fuerzas F1 y F2 y se halla su resultante R12. Esta debe componerse con la fuerza F3, hallando la resultante R123 y así sucesivamente hasta obtener la resultante final R (Fig.3a).
La resultante de las fuerzas se puede obtener mediante la regla del polígono de fuerzas. Para esto, a partir de un punto arbitrario A1(Fig.3b), trazando el vector A1B que representa la fuerza F1 en la escala elegida, desde el punto B, se traza el vector BC, que representa la fuerza F2, así sucesivamente, hasta unir el origen del primer vector con el extremo de la última fuerza, el vector R, representa la resultante del sistema de fuerzas concurrentes. Es fácil comprender que la construcción hecha representa el resultado de la aplicación consecutiva de la regla del triángulo de fuerzas.
El contorno A1BCDE obtenido constituye un polígono, cuyos lados representa todas las fuerzas que actúan en un punto (polígono de fuerzas).
Descomposición de una fuerza en componentes
La descomposición de una fuerza en componentes, significa hallar unas fuerzas tales que estando aplicadas en un mismo punto, efectúan una acción equivalente a la fuerza que se descompone. Con otras palabras, descomponer una fuerza, en componentes, significa hallar tal sistema de fuerzas, que produzca el mismo efecto que la fuerza dada (Ballester, 1995, p.26).
La descomposición de una fuerza dada en dos componentes coplanares, por lo general es un problema indeterminado, es necesario estipular algunas condiciones, para que la solución sea determinada:
- La fijación de dos direcciones, en las cuales deben obrar las componentes.
- La fijación del módulo y dirección de una de las fuerzas componentes.
- La fijación de los módulos de las dos fuerzas componentes.
- La fijación del módulo de una fuerza componente y la dirección de la otra.
Analícese el primer caso, que es el que aparece con mayor frecuencia: Se necesita descomponer la fuerza F en dos fuerzas, las direcciones de las cuales están dadas AM y AN (Fig.4a). El problema se resuelve, trazando desde el extremo de la fuerza F las rectas BC y BD paralelas a las rectas AM y AN respectivamente. Los vectores AC y AD proporcionan, en la misma escala que la fuerza F, las componentes P y Q que se buscan (Fig.4b).
Fuentes
- Ballester Gouraige, Andrés. Fundamentos de Mecánica Teórica y Teoría de los Mecanismos. Editado Departamento E.T.P, I.S.P. "Raúl Gómez García", Guantánamo. 1995.
- Nikitin, E.M. Mecánica Teórica para las escuelas de peritaje. Ed. MIR, Moscú, 1980.
- Sokolov, F y P. Usov. Mecánica Industrial. Tercera edición. Ed. MIR, Moscú, 1986.
- Starzhinski, V.M. Mecánica Teórica. Ed. MIR, Moscú, 1980.
- Targ, S.M. Curso breve de Mecánica Teórica. Cuarta edición. Ed. MIR, Moscú, 1976.