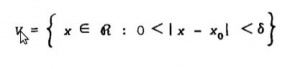Diferencia entre revisiones de «Límite de una función»
m (Texto reemplazado: «<div align="justify">» por «») |
|||
| (No se muestran 8 ediciones intermedias de 5 usuarios) | |||
| Línea 1: | Línea 1: | ||
{{Definición | {{Definición | ||
|nombre=Límite de una función en un punto | |nombre=Límite de una función en un punto | ||
| − | |imagen= | + | |imagen= |
|tamaño= | |tamaño= | ||
|concepto=Como halla el límite de una función en un punto. | |concepto=Como halla el límite de una función en un punto. | ||
| − | }} | + | }} |
| − | '''Límite de una función en un punto | + | '''Límite de una función en un punto.''' Dada una [[Función]] f definida en una vecindad reducida V del [[Punto|punto]] x<sub>0</sub>, se dice que f tiene límite L, cuando x tiende hacia x<sub>0</sub>, si cualquiera sea la [[Sucesiones_numéricas|Sucesión]] {x<sub>0</sub>} de puntos de la vecindad V que converja hacia x<sub>0</sub>, la Sucesión de la [[Imágenes]] {f(x<sub>n</sub>)} converge hacia L. <br /> |
| + | Informalmente, el hecho que una función ''f'' tiene un límite ''L'' en el punto ''c'', significa que el valor de ''f'' puede ser tan cercano a ''L'' como se desee, tomando puntos suficientemente cercanos a ''c'', independientemente de lo que ocurra en ''c''. | ||
| − | == Demostración == | + | == Demostración == |
| − | Para estudiar el comportamiento de una [[Función]] en las cercanías de un [[Punto]] dado, | + | Para estudiar el comportamiento de una [[Función]] en las cercanías de un [[Punto|punto]] dado, considerando una [[Función|función]] f, definida en una vecindad reducida V del punto x<sub>0</sub>:[[Image:Vecindad punto1.JPG|300px|Vecindad punto1.JPG]]<br>Al tomar una Sucesión de puntos de esta vecindad que converja hacia x<sub>0</sub>. Sea dicha Sucesión:<br>A cada x<sub>n</sub> de esta Sucesión está asociada su [[Imagen]] f(x<sub>n</sub>) y así se puden formar la Sucesión de las imágenes:<br>Por tanto se llega a la conclusión que si para cualquier Sucesión de puntos de la vecindad V, que converja hacia x<sub>0</sub>, la Sucesión de las imágenes converge hacia un mismo número L, entonces diremos que L es el límite de la función f, cuando x tiende hacia x<sub>0</sub>.<br> |
| − | == Ejemplo en la convergencia de sucesiones == | + | == Ejemplo en la convergencia de sucesiones == |
| − | + | Considerando una [[función constante]] definida por f(x)=c y sea x<sub>0</sub> un [[Punto|punto]] arbitrario. Entonces, el límite de f cuando x tiende a x<sub>0</sub> es c. | |
| − | + | En efecto, si {x<sub>n</sub>} es una Sucesión que converge hacia x<sub>0</sub>,{f(x<sub>n</sub>)} es la Sucesión de término enésimo f(x<sub>n</sub>)=c, la cual evidentemente converge hacia c, por lo que el límite de f cuando x tiende hacia x<sub>0</sub> es c. | |
| − | + | == Interpretación geométrica == | |
| − | + | Del análisis de estas funciones puede extraerse la idea intuitiva de que el límite de una [[Función|función]] f, cuando x tiende a x<sub>0</sub>, es L si puede lograrse que f(x) esté tan próximo a L como se desee, siempre que se tomen valores de x lo suficiente próximos a x<sub>0</sub>. Esto significa que la distancia entre f(x) y L puede hacerse tan pequeña como se desee y de aquí que para cada número positivo £, por pequeño que este sea, se tenga que: | f(x) - L | < £ "para ciertos valores de x". | |
| − | + | Se puede concluir que para cada £ > 0 se debe encontrar un número ð > 0 de tal forma que para todo x satisfaga<br>0 < | x - x<sub>0</sub> | < ð se tenga | f(x) - L | < £. Si para todo £ > 0 se puede hallar este número ð > 0, se dirá que el límite de la función f cuando x tiende a x<sub>0</sub> es L. | |
| − | + | === Definición geométrica === | |
| − | [[ | + | Dada una [[Función]] f definida en una vecindad reducida del punto x<sub>0</sub>, se dice que f tiene límite L, cuando x tiende hacia x<sub>0</sub>, si para todo número positivo £, existe un número positivo ð, tal que: si 0 < | x - x<sub>0</sub> | < ð entonces | f(x) - L | < £<br>Las dos definiciones anteriores de límite de una [[Función]] son equivalentes. En caso de que se satisfaga cualquiera de ellas, diremos que el límite de una [[Función]] existe cuando x tiende a x<sub>0</sub>. |
| − | === | + | == Fuente == |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * Ministerio de Educación Superior. Departamento de textos y Materiales Didácticos. Análisis Matemático 1. Tomo I. | ||
| + | </div> | ||
[[Category:Análisis_y_Análisis_funcional]] | [[Category:Análisis_y_Análisis_funcional]] | ||
última versión al 20:32 27 ago 2019
| ||||
Límite de una función en un punto. Dada una Función f definida en una vecindad reducida V del punto x0, se dice que f tiene límite L, cuando x tiende hacia x0, si cualquiera sea la Sucesión {x0} de puntos de la vecindad V que converja hacia x0, la Sucesión de la Imágenes {f(xn)} converge hacia L.
Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.
Sumario
Demostración
Para estudiar el comportamiento de una Función en las cercanías de un punto dado, considerando una función f, definida en una vecindad reducida V del punto x0:
Al tomar una Sucesión de puntos de esta vecindad que converja hacia x0. Sea dicha Sucesión:
A cada xn de esta Sucesión está asociada su Imagen f(xn) y así se puden formar la Sucesión de las imágenes:
Por tanto se llega a la conclusión que si para cualquier Sucesión de puntos de la vecindad V, que converja hacia x0, la Sucesión de las imágenes converge hacia un mismo número L, entonces diremos que L es el límite de la función f, cuando x tiende hacia x0.
Ejemplo en la convergencia de sucesiones
Considerando una función constante definida por f(x)=c y sea x0 un punto arbitrario. Entonces, el límite de f cuando x tiende a x0 es c.
En efecto, si {xn} es una Sucesión que converge hacia x0,{f(xn)} es la Sucesión de término enésimo f(xn)=c, la cual evidentemente converge hacia c, por lo que el límite de f cuando x tiende hacia x0 es c.
Interpretación geométrica
Del análisis de estas funciones puede extraerse la idea intuitiva de que el límite de una función f, cuando x tiende a x0, es L si puede lograrse que f(x) esté tan próximo a L como se desee, siempre que se tomen valores de x lo suficiente próximos a x0. Esto significa que la distancia entre f(x) y L puede hacerse tan pequeña como se desee y de aquí que para cada número positivo £, por pequeño que este sea, se tenga que: | f(x) - L | < £ "para ciertos valores de x".
Se puede concluir que para cada £ > 0 se debe encontrar un número ð > 0 de tal forma que para todo x satisfaga
0 < | x - x0 | < ð se tenga | f(x) - L | < £. Si para todo £ > 0 se puede hallar este número ð > 0, se dirá que el límite de la función f cuando x tiende a x0 es L.
Definición geométrica
Dada una Función f definida en una vecindad reducida del punto x0, se dice que f tiene límite L, cuando x tiende hacia x0, si para todo número positivo £, existe un número positivo ð, tal que: si 0 < | x - x0 | < ð entonces | f(x) - L | < £
Las dos definiciones anteriores de límite de una Función son equivalentes. En caso de que se satisfaga cualquiera de ellas, diremos que el límite de una Función existe cuando x tiende a x0.
Fuente
- Ministerio de Educación Superior. Departamento de textos y Materiales Didácticos. Análisis Matemático 1. Tomo I.