Diferencia entre revisiones de «Pendiente de la ecuación de una recta»
(Página creada con '{{Definición|imagen= Pendiente en la ecuación de la recta.jpg}} == '''Pendiente en la ecuación de la recta''' == En la ecuación principal de la recta y = mx + n, el valor ...') (Etiqueta: no tiene enlaces internos) |
|||
| (No se muestran 19 ediciones intermedias de 4 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | {{Definición| | + | {{Definición |
| + | |nombre= Pendiente en la ecuación de la recta | ||
| + | |imagen= Foto_de_la_Pendiente.JPG | ||
| + | |tamaño= 159x166px | ||
| + | |concepto= | ||
| + | }} | ||
== '''Pendiente en la ecuación de la recta''' == | == '''Pendiente en la ecuación de la recta''' == | ||
| − | En la ecuación principal de la recta y = mx + n, el valor de m corresponde a la pendiente de la recta y n es el coeficiente de posición. | + | En la ecuación principal de la recta y = mx + n, el valor de m corresponde a la pendiente de la [[recta]] y n es el coeficiente de posición. |
La pendiente permite obtener el grado de inclinación que tiene una recta, mientras que el coeficiente de posición señala el punto en que la recta interceptará al eje de las ordenadas. | La pendiente permite obtener el grado de inclinación que tiene una recta, mientras que el coeficiente de posición señala el punto en que la recta interceptará al eje de las ordenadas. | ||
En esta ecuación, el valor de n puede ser interpretado como el punto donde la recta intercepta al eje Y, es decir, el valor de y cuando x = 0. Este valor también es llamado coordenada de origen. | En esta ecuación, el valor de n puede ser interpretado como el punto donde la recta intercepta al eje Y, es decir, el valor de y cuando x = 0. Este valor también es llamado coordenada de origen. | ||
Si la pendiente m de una recta y el punto (x0, y0) de la recta son conocidos, entonces la ecuación de la recta puede ser encontrada usando: | Si la pendiente m de una recta y el punto (x0, y0) de la recta son conocidos, entonces la ecuación de la recta puede ser encontrada usando: | ||
| − | + | ||
| + | y - y<sub>o</sub> = m (x - x<sub>o</sub>) | ||
| + | |||
== Ejemplos == | == Ejemplos == | ||
1. Considere una recta que pasa por los puntos (2, 8) y (3, 20). Esta recta tiene pendiente | 1. Considere una recta que pasa por los puntos (2, 8) y (3, 20). Esta recta tiene pendiente | ||
| − | [[image: | + | |
| + | [[image:Tercer_Arreglo.JPG]] | ||
| + | |||
| + | |||
Luego de esto, uno puede definir la ecuación para esta recta usando la fórmula antes mencionada: | Luego de esto, uno puede definir la ecuación para esta recta usando la fórmula antes mencionada: | ||
| − | + | ||
| + | y - 8 = 12 (x - 2) = 12 x - 24 → y = 12 x - 16 | ||
| + | |||
La pendiente de la recta en la fórmula general: | La pendiente de la recta en la fórmula general: | ||
| − | [[image: | + | |
| + | [[image:Cuarto_Arreglo.JPG]] | ||
| + | |||
está dada por: | está dada por: | ||
| − | [[image: | + | |
| + | [[image:Quinto_Arreglo.JPG]] | ||
| + | |||
| + | Una recta que es paralela al eje x tiene pendiente 0 | ||
| + | |||
2. La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo que indica que interceptará al eje y en el punto (0,7). | 2. La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo que indica que interceptará al eje y en el punto (0,7). | ||
En la ecuación general de la recta, la pendiente y el coeficiente de posición quedan determinados por: | En la ecuación general de la recta, la pendiente y el coeficiente de posición quedan determinados por: | ||
| − | [[image: | + | |
| + | [[image:Quinto_Arreglo.JPG]] | ||
| + | |||
| + | [[image:Sexto_Arreglo.JPG]] | ||
| + | |||
| + | == Demostración == | ||
| + | Transformemos la ecuación general de la recta en una ecuación principal. | ||
| + | |||
| + | Ax + By + C = 0 | ||
| − | |||
| − | |||
| − | |||
| − | |||
Ax + By = -C | Ax + By = -C | ||
| + | |||
By = -Ax - C | By = -Ax - C | ||
| − | + | ||
| − | + | [[image:Séptimo_Arreglo.JPG]] | |
| + | |||
| + | [[image:Octavo_Arreglo.JPG]] | ||
| + | |||
donde se demuestran los valores de m y n antes dado. | donde se demuestran los valores de m y n antes dado. | ||
| + | |||
== Ejemplos == | == Ejemplos == | ||
1. ¿Cuál es la pendiente y el coeficiente de posición de la recta 4x - 6y + 3 = 0? | 1. ¿Cuál es la pendiente y el coeficiente de posición de la recta 4x - 6y + 3 = 0? | ||
| − | + | ||
| − | + | [[image:Primer_Arreglo.JPG]] | |
| + | |||
| + | [[image:Acabando_2.JPG]] | ||
| + | |||
2. La pendiente de la recta que pasa por los puntos A(2, 1), B(4, 7) es: | 2. La pendiente de la recta que pasa por los puntos A(2, 1), B(4, 7) es: | ||
| − | [[image: | + | |
| + | [[image:Swgundo_Arreglo.JPG]] | ||
| + | |||
3. La recta que pasa por los puntos A(1, 2), B(1, 7) no tiene pendiente, ya que la división por 0 no está definida. | 3. La recta que pasa por los puntos A(1, 2), B(1, 7) no tiene pendiente, ya que la división por 0 no está definida. | ||
| + | |||
[[image:MRA ejemplo 7.JPG]] | [[image:MRA ejemplo 7.JPG]] | ||
| − | La pendiente de una recta determina su dirección, luego utilizándola se puede decidir sobre el paralelismo y la perpendicularidad de las rectas. | + | |
| + | La pendiente de una recta determina su dirección, luego utilizándola se puede decidir sobre el paralelismo y la [[Paralelismo y Perpendicularidad|perpendicularidad de las rectas]]. | ||
| + | |||
== Fuente == | == Fuente == | ||
| − | * Colectivo de autores. Matemática | + | |
| − | + | * Colectivo de autores. Matemática 11no grado. E | |
| − | + | ||
| − | |||
[[Category:Ecuaciones_funcionales]] | [[Category:Ecuaciones_funcionales]] | ||
última versión al 10:55 11 abr 2013
| ||||
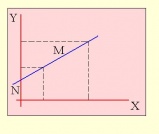
Pendiente en la ecuación de la recta
En la ecuación principal de la recta y = mx + n, el valor de m corresponde a la pendiente de la recta y n es el coeficiente de posición. La pendiente permite obtener el grado de inclinación que tiene una recta, mientras que el coeficiente de posición señala el punto en que la recta interceptará al eje de las ordenadas. En esta ecuación, el valor de n puede ser interpretado como el punto donde la recta intercepta al eje Y, es decir, el valor de y cuando x = 0. Este valor también es llamado coordenada de origen. Si la pendiente m de una recta y el punto (x0, y0) de la recta son conocidos, entonces la ecuación de la recta puede ser encontrada usando:
y - yo = m (x - xo)
Ejemplos
1. Considere una recta que pasa por los puntos (2, 8) y (3, 20). Esta recta tiene pendiente
Luego de esto, uno puede definir la ecuación para esta recta usando la fórmula antes mencionada:
y - 8 = 12 (x - 2) = 12 x - 24 → y = 12 x - 16
La pendiente de la recta en la fórmula general:
está dada por:
Una recta que es paralela al eje x tiene pendiente 0
2. La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo que indica que interceptará al eje y en el punto (0,7). En la ecuación general de la recta, la pendiente y el coeficiente de posición quedan determinados por:
Demostración
Transformemos la ecuación general de la recta en una ecuación principal.
Ax + By + C = 0
Ax + By = -C
By = -Ax - C
donde se demuestran los valores de m y n antes dado.
Ejemplos
1. ¿Cuál es la pendiente y el coeficiente de posición de la recta 4x - 6y + 3 = 0?
2. La pendiente de la recta que pasa por los puntos A(2, 1), B(4, 7) es:
3. La recta que pasa por los puntos A(1, 2), B(1, 7) no tiene pendiente, ya que la división por 0 no está definida.
La pendiente de una recta determina su dirección, luego utilizándola se puede decidir sobre el paralelismo y la perpendicularidad de las rectas.
Fuente
- Colectivo de autores. Matemática 11no grado. E