Diferencia entre revisiones de «Sistema octal»
m (Texto reemplazado: «<div align="justify">» por «») |
|||
| (No se muestran 7 ediciones intermedias de 4 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | == | + | {{Definición |
| − | + | |nombre=Sistema octal | |
| − | + | |imagen=Sistema_octal.jpg | |
| − | + | |tamaño= | |
| − | + | |concepto=El [[sistema numérico]] en base 8 se llama octal y utiliza los dígitos 0 a 7. | |
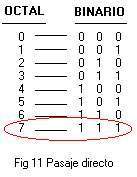
| − | + | }}'''Sistema octal.''' El [[sistema numérico]] en base 8 se llama octal y utiliza los dígitos 0 a 7. Los números octales pueden construirse a partir de números binarios agrupando cada tres dígitos consecutivos de estos últimos (de derecha a izquierda) y obteniendo su valor decimal | |
| − | El [[sistema numérico]] en base 8 se llama octal y utiliza los dígitos 0 a 7. | + | == Descripción == |
| − | Los números octales pueden construirse a partir de números binarios agrupando cada tres dígitos consecutivos de estos últimos (de derecha a izquierda) y obteniendo su valor decimal | + | El [[número binario]] para 74 (en decimal) es 1001010 (en binario), se agruparía como 1 001 010. De modo que el número decimal 74 en octal es 112. En informática, a veces se utiliza la numeración octal en vez de la [[hexadecimal]]. Tiene la ventaja de que no requiere utilizar otros [[símbolos]] diferentes de los dígitos. |
| − | |||
| − | |||
| − | En informática, a veces se utiliza la numeración octal en vez de la [[hexadecimal]]. Tiene la ventaja de que no requiere utilizar otros [[símbolos]] diferentes de los dígitos. | ||
| − | |||
==Fracciones == | ==Fracciones == | ||
| − | |||
La numeración octal es tan buena como la binaria y la hexadecimal para operar con fracciones, puesto que el único factor primo para sus bases es 2. | La numeración octal es tan buena como la binaria y la hexadecimal para operar con fracciones, puesto que el único factor primo para sus bases es 2. | ||
| − | |||
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
|- | |- | ||
| Línea 61: | Línea 55: | ||
==Tabla de conversión entre decimal, binario, hexadecimal y octal== | ==Tabla de conversión entre decimal, binario, hexadecimal y octal== | ||
| − | |||
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
|- | |- | ||
| Línea 220: | Línea 213: | ||
| 16 | | 16 | ||
|} | |} | ||
| − | |||
| − | |||
====Multiplicación==== | ====Multiplicación==== | ||
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
| Línea 315: | Línea 306: | ||
|} | |} | ||
| − | == | + | ==Cambio de base == |
| − | http://ucipedia.uci.cu/index.php/Sistema_octal | + | === De base decimal a base octal === |
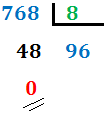
| + | Veamos el método para pasar del sistema decimal al sistema octal mediante un ejemplo. Escribiremos el número 768 (base 10) en base octal (base 8): | ||
| + | |||
| + | '''1. Dividimos el número entre 8:''' | ||
| + | |||
| + | [[Archivo:Octal1.png]] | ||
| + | |||
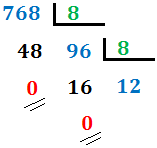
| + | '''2. Si el cociente es mayor o igual que 8, lo dividimos entre 8.''' En nuestro caso, el cociente es 96 (mayor que 8), por lo que lo dividimos de nuevo: | ||
| + | [[Archivo:Octal2.png]] | ||
| + | |||
| + | |||
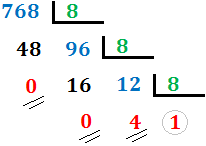
| + | '''3. Continuamos así hasta obtener un cociente menor que 8.''' En nuestro caso, el cociente es 12 (mayor que 8), así que lo dividimos de nuevo: | ||
| + | |||
| + | |||
| + | [[Archivo:Octal3.png]] | ||
| + | |||
| + | |||
| + | El cociente es 1, menor que 8, con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia. | ||
| + | |||
| + | |||
| + | '''4. El número en base 8 es: (Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto) (Primer resto).''' En nuestro caso, el último cociente es 1, el último resto es 4, el penúltimo resto es 0 y el primer resto es 0. Por tanto, el número 768 en base octal es 1400. | ||
| + | |||
| + | === De base octal a base decimal === | ||
| + | |||
| + | El método que seguiremos para pasar un número en base octal a base decimal es: | ||
| + | |||
| + | '''1. De derecha a izquierda:''' multiplicamos la primera cifra por 1 (1 es 8 elevado a 0) ; la segunda, por 8 (8 es 8 elevado a 1); la tercera, por 8 elevado a 2; la cuarta, por 8 elevado a 3. Y así hasta que hayamos multiplicado todas las cifras. | ||
| + | |||
| + | '''2. Sumamos ''' cada uno de los valores obtenidos. | ||
| + | |||
| + | '''Ejemplo:''' pasamos el número 156 (base octal) a base decimal (base 10): | ||
| + | [[Archivo:Octal5.png]] | ||
| + | |||
| + | ==Fuentes== | ||
| + | *[http://ucipedia.uci.cu/index.php/Sistema_octal Sistema octal ''(en ucipedia.uci.cu)''] | ||
| + | *[https://www.matesfacil.com/ESO/sistemas-numeracion/base-octal/sistema-numeracion-octal-base-ocho-ejemplos-teoria-propiedades-cambio-base-decimal-ejercicios-resueltos.html Cambio de base octal/decimal] | ||
[[Category: Matemáticas]] | [[Category: Matemáticas]] | ||
última versión al 21:12 12 ago 2019
| ||||||
Sistema octal. El sistema numérico en base 8 se llama octal y utiliza los dígitos 0 a 7. Los números octales pueden construirse a partir de números binarios agrupando cada tres dígitos consecutivos de estos últimos (de derecha a izquierda) y obteniendo su valor decimal
Sumario
Descripción
El número binario para 74 (en decimal) es 1001010 (en binario), se agruparía como 1 001 010. De modo que el número decimal 74 en octal es 112. En informática, a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos.
Fracciones
La numeración octal es tan buena como la binaria y la hexadecimal para operar con fracciones, puesto que el único factor primo para sus bases es 2.
| Fracción | Octal | Resultado en octal |
|---|---|---|
| 1/2 | 1/2 | 0,4 |
| 1/3 | 1/3 | 0,25252525 periódico |
| 1/4 | 1/4 | 0,2 |
| 1/5 | 1/5 | 0,14631463 periódico |
| 1/6 | 1/6 | 0,125252525 periódico |
| 1/7 | 1/7 | 0,111111 periódico |
| 1/8 | 1/10 | 0,1 |
| 1/9 | 1/11 | 0,07070707 periódico |
| 1/10 | 1/12 | 0,063146314 periódico |
Tabla de conversión entre decimal, binario, hexadecimal y octal
| Decimal | Binario | Hexadecimal | octal |
|---|---|---|---|
| 0 | 00000 | 0 | 0 |
| 1 | 00001 | 1 | 1 |
| 2 | 00010 | 2 | 2 |
| 3 | 00011 | 3 | 3 |
| 4 | 00100 | 4 | 4 |
| 5 | 00101 | 5 | 5 |
| 6 | 00110 | 6 | 6 |
| 7 | 00111 | 7 | 7 |
| 8 | 01000 | 8 | 10 |
| 9 | 01001 | 9 | 11 |
| 10 | 01010 | A | 12 |
Operaciones
Adición
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Multiplicación
| * | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
| 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
Cambio de base
De base decimal a base octal
Veamos el método para pasar del sistema decimal al sistema octal mediante un ejemplo. Escribiremos el número 768 (base 10) en base octal (base 8):
1. Dividimos el número entre 8:
2. Si el cociente es mayor o igual que 8, lo dividimos entre 8. En nuestro caso, el cociente es 96 (mayor que 8), por lo que lo dividimos de nuevo:
3. Continuamos así hasta obtener un cociente menor que 8. En nuestro caso, el cociente es 12 (mayor que 8), así que lo dividimos de nuevo:
El cociente es 1, menor que 8, con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.
4. El número en base 8 es: (Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto) (Primer resto). En nuestro caso, el último cociente es 1, el último resto es 4, el penúltimo resto es 0 y el primer resto es 0. Por tanto, el número 768 en base octal es 1400.
De base octal a base decimal
El método que seguiremos para pasar un número en base octal a base decimal es:
1. De derecha a izquierda: multiplicamos la primera cifra por 1 (1 es 8 elevado a 0) ; la segunda, por 8 (8 es 8 elevado a 1); la tercera, por 8 elevado a 2; la cuarta, por 8 elevado a 3. Y así hasta que hayamos multiplicado todas las cifras.
2. Sumamos cada uno de los valores obtenidos.
Ejemplo: pasamos el número 156 (base octal) a base decimal (base 10):
![]()