Diferencia entre revisiones de «Círculo»
| Línea 1: | Línea 1: | ||
| − | {{Definición|Nombre=Círculo|imagen=Círculo.JPG|concepto=Porción de un [[plano]] limitado por una circunferencia.}}'''Círculo(Figura). '''En Geometría, superficie plana definida por una [[Circunferencia|circunferencia]]. Aunque ambos conceptos están relacionados, no se debe confundir la circunferencia (curva) con el círculo (superficie).<br>De todas las figuras planas con igual perímetro, el círculo es la de mayor área. El cociente entre la longitud de una circunferencia y su diámetro es una constante que se representa como pi.<br> | + | {{Definición|Nombre=Círculo|imagen=Círculo.JPG|concepto=Porción de un [[plano]] limitado por una circunferencia.}}'''Círculo(Figura). |
| + | <div align="justify"> | ||
| + | '''En Geometría, superficie plana definida por una [[Circunferencia|circunferencia]]. Aunque ambos conceptos están relacionados, no se debe confundir la circunferencia (curva) con el círculo (superficie).<br>De todas las figuras planas con igual perímetro, el círculo es la de mayor área. El cociente entre la longitud de una circunferencia y su diámetro es una constante que se representa como pi.<br> | ||
<br> | <br> | ||
| Línea 17: | Línea 19: | ||
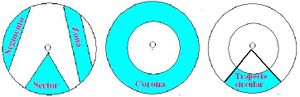
<br>'''Sector circular''': Parte del círculo comprendida por un arco y los dos radios que determinan sus extremos.<br>'''Segmento circular''': Parte del círculo limitada por un arco y su cuerda.<br>'''Anillo o Corona''': Porción del plano limitada por dos circunferencias que tienen el mismo centro. <br>Trapecio circular: Porción de Anillo o Corona limitada por dos radios.<br> | <br>'''Sector circular''': Parte del círculo comprendida por un arco y los dos radios que determinan sus extremos.<br>'''Segmento circular''': Parte del círculo limitada por un arco y su cuerda.<br>'''Anillo o Corona''': Porción del plano limitada por dos circunferencias que tienen el mismo centro. <br>Trapecio circular: Porción de Anillo o Corona limitada por dos radios.<br> | ||
| − | == [[Image:Círculo elementos.JPG|thumb|center|Algunos elementos del Círculo]] | + | ==Área<br>== |
| + | [[Image:Círculo elementos.JPG|thumb|center|Algunos elementos del Círculo]] | ||
A diferencia de la circunferencia, el círculo posee área como las demás figuras geométricas. Esta se calcula a través de la siguiente fórmula:<br>A = Pi * r<sup>2</sup> Siendo r el radio de la circunferencia. | A diferencia de la circunferencia, el círculo posee área como las demás figuras geométricas. Esta se calcula a través de la siguiente fórmula:<br>A = Pi * r<sup>2</sup> Siendo r el radio de la circunferencia. | ||
Revisión del 12:10 1 abr 2011
| ||||||
Círculo(Figura).
En Geometría, superficie plana definida por una circunferencia. Aunque ambos conceptos están relacionados, no se debe confundir la circunferencia (curva) con el círculo (superficie).
De todas las figuras planas con igual perímetro, el círculo es la de mayor área. El cociente entre la longitud de una circunferencia y su diámetro es una constante que se representa como pi.
Elementos esenciales
Los elementos de la circunferencia, tales como: centro, radio, diámetro, cuerda, tangente y secante, se consideran también como pertenecientes al círculo, y así, todo círculo, al igual que la circunferencia correspondiente se nombra por la letra de su centro.
Además de estos, el círculo tiene también otros elementos:
Sector circular: Parte del círculo comprendida por un arco y los dos radios que determinan sus extremos.
Segmento circular: Parte del círculo limitada por un arco y su cuerda.
Anillo o Corona: Porción del plano limitada por dos circunferencias que tienen el mismo centro.
Trapecio circular: Porción de Anillo o Corona limitada por dos radios.
Área
A diferencia de la circunferencia, el círculo posee área como las demás figuras geométricas. Esta se calcula a través de la siguiente fórmula:
A = Pi * r2 Siendo r el radio de la circunferencia.
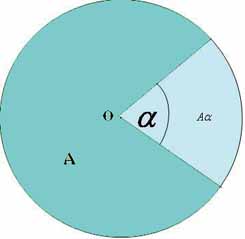
Sector circular
El área del sector circular que se puede apreciar en la figura, depende del valor del ángulo central y del área del círculo A. Se puede calcular a través de la siguiente fórmula:
Ver también
Fuentes
- Microsoft ® Encarta ® 2007. © 1993--2006 Microsoft Corporation. Reservados todos los derechos.
- Miyares Arturo y Escalona Jose M. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974.