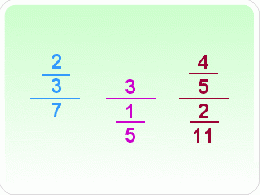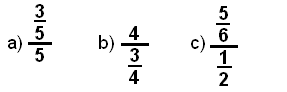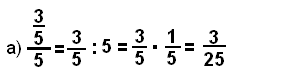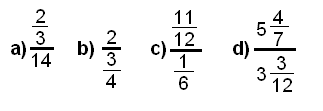Diferencia entre revisiones de «Fracción compleja»
| Línea 8: | Línea 8: | ||
'''Fracción compleja'''. Es una [[división]] indicada; cuando efectuamos dicha operación decimos que hemos simplificado la fracción compleja. | '''Fracción compleja'''. Es una [[división]] indicada; cuando efectuamos dicha operación decimos que hemos simplificado la fracción compleja. | ||
== Antecedentes == | == Antecedentes == | ||
| − | La teoría y el cálculo de las [[fracciones]] como la utilizamos en la actualidad, se le atribuye al matemático hindú Brahmagupta (600 años a.n.e.). Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con [[fracciones]] de una forma más simple. | + | La teoría y el cálculo de las [[fracciones]] como la utilizamos en la actualidad, se le atribuye al matemático hindú Brahmagupta (600 años a.n.e.).<br> Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con [[fracciones]] de una forma más simple. |
== Fracción compleja == | == Fracción compleja == | ||
| − | Una fracción es una [[división]] indicada. | + | Una [[fracciones|fracción]] es una [[división]] indicada. |
[[Archivo:Dibujo 01.PNG]] | [[Archivo:Dibujo 01.PNG]] | ||
| − | En consecuencia, toda [[división]] se puede indicar en forma de fracción. | + | En consecuencia, toda [[división]] se puede indicar en forma de [[fracciones|fracción]].<br> |
Consideremos estos ejemplos: | Consideremos estos ejemplos: | ||
| Línea 23: | Línea 23: | ||
Cada inciso es una [[división]] indicada en la que el dividendo es el numerador y el divisor es el denominador. Se usa una raya mayor para separar los términos y distinguirla así de la raya de la fracción de las [[fracciones]] dadas. | Cada inciso es una [[división]] indicada en la que el dividendo es el numerador y el divisor es el denominador. Se usa una raya mayor para separar los términos y distinguirla así de la raya de la fracción de las [[fracciones]] dadas. | ||
| − | a) el numerador es una fracción, el denominador es un [[número natural]]. Efectúa la [[división]] indicada: | + | a) el numerador es una [[fracciones|fracción]], el denominador es un [[número natural]]. Efectúa la [[división]] indicada: |
[[Archivo:Dibujo 03.PNG]] | [[Archivo:Dibujo 03.PNG]] | ||
| − | b) el numerador es un [[número natural]], el denominador es una fracción; procedes de la misma forma. | + | b) el numerador es un [[número natural]], el denominador es una [[fracciones|fracción]]; procedes de la misma forma. |
[[Archivo:Dibujo 04.PNG]] | [[Archivo:Dibujo 04.PNG]] | ||
Revisión del 14:43 8 ago 2012
| ||||||
Fracción compleja. Es una división indicada; cuando efectuamos dicha operación decimos que hemos simplificado la fracción compleja.
Antecedentes
La teoría y el cálculo de las fracciones como la utilizamos en la actualidad, se le atribuye al matemático hindú Brahmagupta (600 años a.n.e.).
Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con fracciones de una forma más simple.
Fracción compleja
Una fracción es una división indicada.
En consecuencia, toda división se puede indicar en forma de fracción.
Consideremos estos ejemplos:
Halla el cociente:
Cada inciso es una división indicada en la que el dividendo es el numerador y el divisor es el denominador. Se usa una raya mayor para separar los términos y distinguirla así de la raya de la fracción de las fracciones dadas.
a) el numerador es una fracción, el denominador es un número natural. Efectúa la división indicada:
b) el numerador es un número natural, el denominador es una fracción; procedes de la misma forma.
c) en este inciso ambos términos son fracciones.
En los incisos b) y c) has obtenido como cociente una fracción impropia, puedes también dar el resultado como número mixto.
Definición
Las fracciones que tienen fracciones en su numerador, en su denominador, o en ambos términos a la vez se denominan fracciones complejas.
Ejercicios
Halla el cociente:
Referencias
Fuentes
- Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, edición 1990.
- Fracción compleja