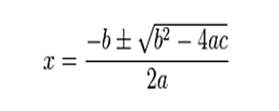Diferencia entre revisiones de «Ecuación de segundo grado»
m (→Ejemplos: (mejorando formato)) |
m (→Formula de resolución de la ecuación de segundo grado) |
||
| Línea 13: | Línea 13: | ||
== Formula de resolución de la ecuación de segundo grado == | == Formula de resolución de la ecuación de segundo grado == | ||
| − | + | Las soluciones de una ecuación de segundo grado en la forma general ax<sup>2</sup> + bx + c = 0 vienen dadas por la '''fórmula cuadrática''': | |
| + | |||
| + | [[Image:Formula 1.jpg]] | ||
| + | |||
| + | Al radicando de fórmula, ''D = b<sup>2</sup> - 4·a·c'', se le denomina '''discriminante''' de la ecuación. El número (y tipo) de soluciones queda determinado por el signo del discriminante<ref>[https://www.matesfacil.com/resueltos-ecuaciones-segundo-grado.htm Ecuaciones de segundo grado completas], (Matesfacil.com).</ref> | ||
| + | |||
| + | == Tipos de soluciones == | ||
| + | |||
| + | |||
*Caso 1: D > 0 | *Caso 1: D > 0 | ||
| Línea 35: | Línea 43: | ||
Sin embargo, se puede escribir x<sub>1 </sub> = (-b +i |D |<sup>1/2 </sup>)/2a , x<sub>2 </sub> = (-b -i |D |<sup>1/2 </sup>)/2a, donde i<sup>2 </sup> = -1.Las dos raíces son números complejos conjugados. | Sin embargo, se puede escribir x<sub>1 </sub> = (-b +i |D |<sup>1/2 </sup>)/2a , x<sub>2 </sub> = (-b -i |D |<sup>1/2 </sup>)/2a, donde i<sup>2 </sup> = -1.Las dos raíces son números complejos conjugados. | ||
| − | Aun en el caso de que los coeficientes sean números complejos existen , exactamente, dos raíces complejas pero no son conjugados. Habrá que hallar raíz de un número complejo. | + | Aun en el caso de que los coeficientes sean números complejos existen , exactamente, dos raíces complejas pero no son conjugados. Habrá que hallar raíz de un número complejo. |
| + | |||
| + | == Referencias == | ||
| + | {{listaref|2}} | ||
== Algoritmo de resolución == | == Algoritmo de resolución == | ||
Revisión del 04:48 30 nov 2016
| ||||
Ecuación de segundo grado. Toda ecuación de la forma ax2+bx+c=0 (a, b, c Є R, a ≠ 0) se denomina ecuación de segundo grado o cuadrática. La ecuación es completa si los tres coeficientes (a, b y c) son distintos de cero. Si algunos de los coeficientes b y c es igual a 0, entonces la ecuación es incompleta .
Sumario
Resolución
Algunas ecuaciones de segundo grado se resuelven fácilmente aplicando la Descomposición factorial y la siguiente propiedad de los Números reales:
- Para todos los números reales a y b se cumple a • b = 0 si y solo si a = 0 o b = 0.
Formula de resolución de la ecuación de segundo grado
Las soluciones de una ecuación de segundo grado en la forma general ax2 + bx + c = 0 vienen dadas por la fórmula cuadrática:
Al radicando de fórmula, D = b2 - 4·a·c, se le denomina discriminante de la ecuación. El número (y tipo) de soluciones queda determinado por el signo del discriminante[1]
Tipos de soluciones
- Caso 1: D > 0
- Caso 2: D = 0
(x + b/2a)2 = 0 La solución de la ecuación es x1,2 = - b/2a
( raíz doble)
- Caso 3: D < 0
En este caso el número b2 - 4ac es negativo y no es posible la extracción de su raíz cuadrada en el dominio de los números reales. Por consiguiente la ecuación ax2 + bx + c = 0 (a ≠ 0) no tiene soluciones reales si D < 0.
Sin embargo, se puede escribir x1 = (-b +i |D |1/2 )/2a , x2 = (-b -i |D |1/2 )/2a, donde i2 = -1.Las dos raíces son números complejos conjugados.
Aun en el caso de que los coeficientes sean números complejos existen , exactamente, dos raíces complejas pero no son conjugados. Habrá que hallar raíz de un número complejo.
Referencias
- ↑ Ecuaciones de segundo grado completas, (Matesfacil.com).
Algoritmo de resolución
Para resolver una ecuación cuadrática después de expresada ax2 + bx + c = 0 (a ≠ 0), puedes utilizar el algoritmo siguiente: 1. Identifica los cocientes a, b y c 2. Sustituye los valores en la formula del discriminante D = b2 - 4ac. 3. Si D < 0, entonces no posee soluciones reales y finaliza. 4. Si D = 0, entonces posee una sola solución x = - b/2ª
Ejemplos
Son ecuaciones de segundo grado los siguientes ejemplos
- x2 - 2x + 35 = 0
- 4x2 – 9 = 0
- 2x2 = 0
Hay ecuaciones que mediante transformaciones algebraicas se transforman en ecuaciones cuadráticas, por ejemplo
- x2 = x + 3
- 2x2 = 8
- (x - 2)(x + 1) = 10
Fuente
- Libro de texto Matemática 9no grado, Editorial Pueblo y Educación, 2001