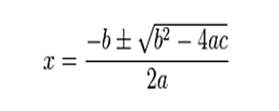Diferencia entre revisiones de «Ecuación de segundo grado»
| Línea 2: | Línea 2: | ||
{{Definición | {{Definición | ||
|nombre= Ecuaciones de Segundo Grado | |nombre= Ecuaciones de Segundo Grado | ||
| − | |concepto=Toda ecuación de la forma <math> | + | |concepto=Toda ecuación de la forma <math>ax^2 + b x + c = 0</math> (a, b, c Є R, a ≠ 0)}} |
<div align="justify"> | <div align="justify"> | ||
'''Ecuaciones de segundo grado'''. Toda ecuación de la forma <math>a*x_2 + b*x + c = 0</math> (a, b, c Є R, a ≠ 0) se denomina ecuación de segundo grado o cuadrática. | '''Ecuaciones de segundo grado'''. Toda ecuación de la forma <math>a*x_2 + b*x + c = 0</math> (a, b, c Є R, a ≠ 0) se denomina ecuación de segundo grado o cuadrática. | ||
| Línea 14: | Línea 14: | ||
== Formula de resolución de la ecuación de segundo grado == | == Formula de resolución de la ecuación de segundo grado == | ||
| − | Considerando la ecuación general | + | Considerando la ecuación general ax<sup>2</sup> + bx + c = 0 (a ≠ 0) se descompone en factores el miembro izquierdo, para ello se divide ambos miembros de la ecuación por a y se adiciona a cada uno la expresión (b/2a)2 para transformar el miembro izquierdo en un [[Trinomio cuadrado perfecto]] ax2 + bx + c = 0 x2 + bx/a + c/a = 0 x2 + b/a x + c/a + (b/2a)2 = (b/2a)2 x2 + b/a x + (b/2a)2 = (b/2a)2 - c/a (x + b/2a)2 = (b2 - 4ac)/4a2 En la expresión (b2 - 4ac)/4a2 se cumple siempre que 4a2 > 0, pero b2 - 4ac puede ser positivo, cero o negativo, luego hagamos D = b2 - 4ac, considerando los casos siguientes: |
*Caso 1: D > 0 | *Caso 1: D > 0 | ||
| − | [[Image:Formula 1.jpg|thumb|left | + | [[Image:Formula 1.jpg|thumb|left]]'''Fórmula General de Resolución de la Ecuación de Segundo Grado<br>''' |
<br> | <br> | ||
Revisión del 18:58 29 mar 2011
| ||||
Ecuaciones de segundo grado. Toda ecuación de la forma <math>a*x_2 + b*x + c = 0</math> (a, b, c Є R, a ≠ 0) se denomina ecuación de segundo grado o cuadrática.
Sumario
Resolución
Algunas ecuaciones de segundo grado se resuelven fácilmente aplicando la Descomposición factorial y la siguiente propiedad de los Números reales:
- Para todos los números reales a y b se cumple a • b = 0 si y solo si a = 0 o b = 0.
Formula de resolución de la ecuación de segundo grado
Considerando la ecuación general ax2 + bx + c = 0 (a ≠ 0) se descompone en factores el miembro izquierdo, para ello se divide ambos miembros de la ecuación por a y se adiciona a cada uno la expresión (b/2a)2 para transformar el miembro izquierdo en un Trinomio cuadrado perfecto ax2 + bx + c = 0 x2 + bx/a + c/a = 0 x2 + b/a x + c/a + (b/2a)2 = (b/2a)2 x2 + b/a x + (b/2a)2 = (b/2a)2 - c/a (x + b/2a)2 = (b2 - 4ac)/4a2 En la expresión (b2 - 4ac)/4a2 se cumple siempre que 4a2 > 0, pero b2 - 4ac puede ser positivo, cero o negativo, luego hagamos D = b2 - 4ac, considerando los casos siguientes:
- Caso 1: D > 0
- Caso 2: D = 0
(x + b/2a)2 = 0 La solución de la ecuación es x = - b/2a
- Caso 3: D < 0
En este caso el número b2 - 4ac es negativo y no es posible la extracción de su raíz cuadrada en el dominio de los números reales. Por consiguiente la ecuación ax2 + bx + c = 0 (a ≠ 0) no tiene soluciones reales si D < 0.
Algoritmo de resolución
Para resolver una ecuación cuadrática después de expresada ax2 + bx + c = 0 (a ≠ 0), puedes utilizar el algoritmo siguiente: 1. Identifica los cocientes a, b y c 2. Sustituye los valores en la formula del discriminante D = b2 - 4ac. 3. Si D < 0, entonces no posee soluciones reales y finaliza. 4. Si D = 0, entonces posee una sola solución x = - b/2ª
Ejemplos
Son ecuaciones de segundo grado los siguientes ejemplos
- x2 - 2x + 35 = 0
- 4x2 – 9 = 0
- 2x2 = 0
Hay ecuaciones que mediante transformaciones algebraicas se transforman en ecuaciones cuadráticas, por ejemplo
- x2 = x + 3
- 2x2 = 8
- (x - 2)(x + 1) = 10
Fuente
- Libro de texto Matemática 9no grado, Editorial Pueblo y Educación, 2001