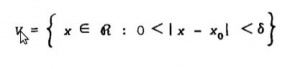Diferencia entre revisiones de «Límite de una función»
| Línea 4: | Línea 4: | ||
|tamaño= | |tamaño= | ||
|concepto=Como halla el límite de una función en un punto. | |concepto=Como halla el límite de una función en un punto. | ||
| − | }} | + | }} |
<div align="justify"> | <div align="justify"> | ||
| − | + | '''Límite de una función en un punto.''' Dada una [[Función]] f definida en una vecindad reducida V del [[Punto(geometría)]] x<sub>0</sub>, se dice que f tiene límite L, cuando x tiende hacia x<sub>0</sub>, si cualquiera sea la [[Sucesiones_numéricas|Sucesión]] {x<sub>0</sub>} de puntos de la vecindad V que converja hacia x<sub>0</sub>, la Sucesión de la [[Imágenes]] {f(x<sub>n</sub>)} converge hacia L. | |
| − | '''Límite de una función en un punto.''' Dada una [[Función]] f definida en una vecindad reducida V del [[Punto(geometría)]] x<sub>0</sub>, se dice que f tiene límite L, cuando x tiende hacia x<sub>0</sub>, si cualquiera sea la [[Sucesión]] {x<sub>0</sub>} de puntos de la vecindad V que converja hacia x<sub>0</sub>, la | ||
== Demostración == | == Demostración == | ||
| Línea 36: | Línea 35: | ||
Ministerio de Educación Superior. Departamento de textos y [[Materiales]] Didácticos. [[Análisis]] Matemático 1 Tomo I | Ministerio de Educación Superior. Departamento de textos y [[Materiales]] Didácticos. [[Análisis]] Matemático 1 Tomo I | ||
| − | + | </div> | |
[[Category:Análisis_y_Análisis_funcional]] | [[Category:Análisis_y_Análisis_funcional]] | ||
Revisión del 12:58 5 abr 2011
| ||||||
Límite de una función en un punto. Dada una Función f definida en una vecindad reducida V del Punto(geometría) x0, se dice que f tiene límite L, cuando x tiende hacia x0, si cualquiera sea la Sucesión {x0} de puntos de la vecindad V que converja hacia x0, la Sucesión de la Imágenes {f(xn)} converge hacia L.
Sumario
Demostración
Para estudiar el comportamiento de una Función en las cercanías de un Punto dado, consideremos una Función f, definida en una vecindad reducida V del punto x0:
Tomemos una Sucesión de puntos de esta vecindad que converja hacia x0. Sea dicha Sucesión:Sucesión límite1.JPG
A cada xn de esta Sucesión está asociada su Imagen f(xn) y así podemos formar la Sucesión de las imágenes:Archivo:Sucesion imágenes límite1.JPG
Por tanto llegamos a la conclusión que si para cualquier Sucesión de puntos de la vecindad V, que converja hacia x0, la Sucesión de las imágenes converge hacia un mismo número L, entonces diremos que L es el límite de la función f, cuando x tiende hacia x0.
Ejemplo en la convergencia de sucesiones
Consideremos una Función Constante definida por f(x)=c y sea x0 un Punto arbitrario. Entonces, el límite de f cuando x tiende a x0 es c.
En efecto, si {xn} es una Sucesión que converge hacia x0,{f(xn)} es la Sucesión de término enésimo f(xn)=c, la cual evidentemente converge hacia c, por lo que el límite de f cuando x tiende hacia x0 es c.
Interpretación geométrica
Del Análisis de estas funciones puede extraerse la idea intuitiva de que el límite de una Función f, cuando x tiende a x0, es L si puede lograrse que f(x) esté tan próximo a L como se desee, siempre que se tomen valores de x lo suficiente próximos a x0. Esto significa que la distancia entre f(x) y L puede hacerse tan pequeña como se desee y de aquí que para cada número positivo £, por pequeño que este sea, se tenga que: | f(x) - L | < £ "para ciertos valores de x".
Podemos concluir que para cada £ > 0 debemos encontrar un número ð > 0 de tal forma que para todo x satisfaga
0 < | x - x0 | < ð se tenga | f(x) - L | < £. Si para todo £ > 0 se puede hallar este número ð > 0, diremos que el límite de la función f cuando x tiende a x0 es L.
Definición Geométrica
Dada una Función f definida en una vecindad reducida del punto x0, se dice que f tiene límite L, cuando x tiende hacia x0, si para todo número positivo £, existe un número positivo ð, tal que: si 0 < | x - x0 | < ð entonces | f(x) - L | < £
Las dos definiciones anteriores de límite de una Función son equivalentes. En caso de que se satisfaga cualquiera de ellas, diremos que el límite de una Función existe cuando x tiende a x0.
Fuentes
Ministerio de Educación Superior. Departamento de textos y Materiales Didácticos. Análisis Matemático 1 Tomo I