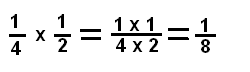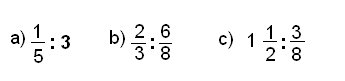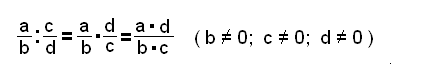Diferencia entre revisiones de «Multiplicación y división de fracciones comunes»
(→Multiplicación y división de fracciones comunes.) |
|||
| Línea 40: | Línea 40: | ||
[[Archivo:imagen 6.PNG]] | [[Archivo:imagen 6.PNG]] | ||
| − | En todos los casos se han multiplicado las fracciones multiplicando | + | En todos los casos se han multiplicado las fracciones multiplicando numerador por numerador y denominador por denominador. |
'''Veamos otros ejemplos:''' | '''Veamos otros ejemplos:''' | ||
| Línea 63: | Línea 63: | ||
[[Archivo:imagen 11.PNG]] | [[Archivo:imagen 11.PNG]] | ||
| − | == Recíproco de una fracción | + | == Recíproco de una fracción == |
Antes de comenzar el estudio de la división de fracciones, es necesario que aprendas qué es el recíproco de una fracción, lo necesitarás en el procedimiento a seguir para dividir. | Antes de comenzar el estudio de la división de fracciones, es necesario que aprendas qué es el recíproco de una fracción, lo necesitarás en el procedimiento a seguir para dividir. | ||
| Línea 74: | Línea 74: | ||
| − | == Ejemplos | + | == Ejemplos == |
Halla el recíproco de: | Halla el recíproco de: | ||
| Línea 108: | Línea 108: | ||
| − | == División de fracciones comunes | + | == División de fracciones comunes == |
En los números naturales la división significa repartir en partes iguales, con las fracciones también se le puede dar esa interpretación y resolver situaciones prácticas, por ejemplo: | En los números naturales la división significa repartir en partes iguales, con las fracciones también se le puede dar esa interpretación y resolver situaciones prácticas, por ejemplo: | ||
| Línea 133: | Línea 133: | ||
| − | == | + | == Ejemplos == |
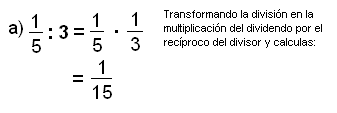
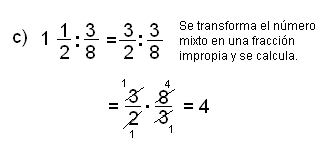
Halla el cociente: | Halla el cociente: | ||
| Línea 150: | Línea 150: | ||
| − | == En resumen | + | == En resumen == |
La división de fracciones se realiza transformándola en una multiplicación en la cual el primer factor es el dividendo y el segundo es el recíproco del divisor. Luego se procede como en la multiplicación. | La división de fracciones se realiza transformándola en una multiplicación en la cual el primer factor es el dividendo y el segundo es el recíproco del divisor. Luego se procede como en la multiplicación. | ||
Revisión del 08:21 26 may 2011
Sumario
Antecedentes
La teoría y el cálculo de las fracciones como la utilizamos en la actualidad, se le atribuye al matemático hindú Brahmagupta (600 años a.n.e.). Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con fracciones de una forma más simple.
Multiplicación y división de fracciones comunes
Al igual que los números naturales, las fracciones se pueden multiplicar. Por ejemplo: Si quieres saber el tiempo que inviertes en practicar la ortografía dedicando ¼ (un cuarto) de hora 3 veces a la semana, ¿cómo lo planteas?.
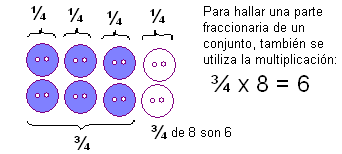
¿Necesitas conocer cuántos botones representan ¾ (tres cuartas) partes de un conjunto de 8 botones?
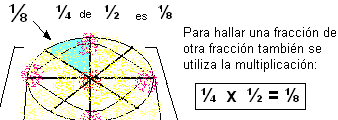
¿Quieres saber qué parte del pastel se comió tu hermanita si le sirvieron ¼ (un cuarto) de la mitad del pastel?
En los ejemplos anteriores has visto diferentes representaciones para la multiplicación de fracciones, en todos los casos el producto se calcula de la misma forma:
Observa que:
En todos los casos se han multiplicado las fracciones multiplicando numerador por numerador y denominador por denominador.
Veamos otros ejemplos:
Halla el producto de las siguientes fracciones:
¿Cómo los resolvemos?:
En resumen: La multiplicación de fracciones se realiza multiplicando los numeradores y multiplicando los denominadores entre sí. Es conveniente, antes de calcular el producto simplificar tanto como sea posible de lo contrario deberás hacerlo en la fracción resultante.
En general:
Recíproco de una fracción
Antes de comenzar el estudio de la división de fracciones, es necesario que aprendas qué es el recíproco de una fracción, lo necesitarás en el procedimiento a seguir para dividir.
Definición 1
El recíproco de una fracción es la fracción
donde
.
Dada una fracción, para formar su recíproco, basta invertir sus términos.
Ejemplos
Halla el recíproco de:
a) _1_
3
b) 2
c) _7_
4
d) 0,5
Respuestas:
a) _1_ igual a _3_ Invirtiendo el numerador y el denominador.
3 1 El recíproco de _1_ es 3.
3
b) 2 igual a ½ El recíproco de 2 es ½ (un medio).
c) _7_ igual a _4_ El recíproco de _7_ es _4_.
4 7 4 7
d) 0,5 igual a _5_ Se escribe la expresión decimal como fracción.
10 El recíproco de _5_ es _10_ = 2.
10 5
División de fracciones comunes
En los números naturales la división significa repartir en partes iguales, con las fracciones también se le puede dar esa interpretación y resolver situaciones prácticas, por ejemplo: Tienes 5 naranjas y las picas exactamente a la mitad ¿cuántas partes tienes ahora?
La mitad de un huerto escolar la divides en cuatro partes iguales para sembrar lechugas en una de ellas, ¿qué parte del terreno se dedicará a ese tipo de hortalizas?
Para hallar qué parte es un conjunto de otro, debes dividir. Luego también podemos darle este significado a la división de fracciones , por ejemplo:
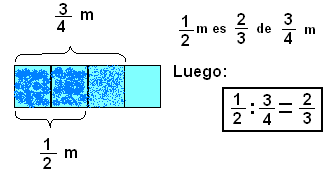
¿Qué parte es ½ m de tela de ¾ m?
Independientemente de las diferentes interpretaciones que puede tener la división, para calcular existe un único procedimiento como podemos observar a continuación:
En todos los casos se han dividido las fracciones reduciéndolas a una multiplicación donde el segundo factor es el recíproco del divisor.
Ejemplos
Halla el cociente:
Para resolverlos:
En resumen
La división de fracciones se realiza transformándola en una multiplicación en la cual el primer factor es el dividendo y el segundo es el recíproco del divisor. Luego se procede como en la multiplicación.
En general:
Fuentes
- Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, 1990.
- `Profesorenlinea.cl