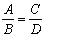Diferencia entre revisiones de «Teorema de Tales»
| Línea 1: | Línea 1: | ||
| + | {{Normalizar|motivo=texto}} | ||
{{Desarrollo}} | {{Desarrollo}} | ||
{{Definición|Nombre=Teorema de Tales|imagen=Teorema_Tales.JPG|concepto= La igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triágulos.}}<div align="justify"> | {{Definición|Nombre=Teorema de Tales|imagen=Teorema_Tales.JPG|concepto= La igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triágulos.}}<div align="justify"> | ||
Revisión del 13:38 15 jul 2011
Teorema de Tales. Es la división de un segmento en partes iguales y también en partes proporcionales a números dados.
Sumario
Historia
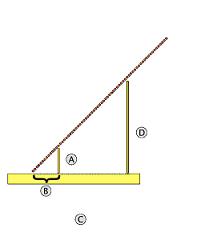
Según la leyenda (relatada por Plutarco ), Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (conocidas como Keops, Kefrén y Micerinos), construidas varios siglos antes. Admirado ante tan portentosos monumentos de esta civilización, quiso saber su altura. De acuerdo a la leyenda, trató este problema con semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos), pudo establecer una relación de semejanza (teorema primero de Tales) entre dos triángulos rectángulos, por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (conocible) y la longitud de su altura (desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) cuyos catetos conocibles (A y B) son, la longitud de la vara y la longitud de su sombra. Realizando las mediciones en una hora del día en que la sombra de la vara sea perpendicular a la base de la cara desde la cual medía la sombra de la pirámide y agregando a su sombra la mitad de la longitud de una de las caras, obtenía la longitud total C de la sombra de la pirámide hasta el centro de la misma.
Teorema de Tales (primero)
Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
Corolario
Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:
Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la pirámide de Keops en Egipto. En cualquier caso, el teorema per se demuestra la semejanza entre dos triángulos, no la constancia del cociente. Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo): Si las rectas a, b, c son paralelas y cortan a otras dos rectas r y s, entonces los segmentos que determinan en ellas son proporcionales.
Teorema de Tales (segundo)
Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el ángulo ABC, es recto.