Diferencia entre revisiones de «Triángulo»
| Línea 1: | Línea 1: | ||
| − | {{Definición|Nombre=Triángulo|imagen=Triángulo.JPG|concepto=Es la porción de plano limitada por una línea poligonal cerrada de tres lados, o sea, la parte de superficie plana limitada por tres segmentos.}}'''Triángulo(figura)''': Polígono de tres lados. La suma de los tres ángulos de un triángulo es 180º. Dos de los ángulos son, necesariamente, agudos. El tercero puede ser también agudo, o bien recto u obtuso.<br> | + | {{Definición|Nombre=Triángulo|imagen=Triángulo.JPG|concepto=Es la porción de plano limitada por una línea poligonal cerrada de tres lados, o sea, la parte de superficie plana limitada por tres segmentos.}}'''Triángulo(figura)''': Polígono de tres lados. La suma de los tres ángulos de un triángulo es 180º. Dos de los ángulos son, necesariamente, agudos. El tercero puede ser también agudo, o bien recto u obtuso.<br> |
| − | <br> | + | <br> |
| − | == '''Clasificación'''<br> == | + | == '''Clasificación'''<br> == |
| − | Los triángulos se clasifican según la longitud de sus lados, o según la amplitud de sus ángulos. | + | Los triángulos se clasifican según la longitud de sus lados, o según la amplitud de sus ángulos. |
| − | === Según sus lados<br> === | + | === Según sus lados<br> === |
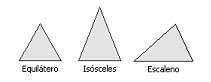
| − | Según la longitud de sus lados, los triángulos se clasifican en equiláteros, si sus tres lados son iguales, isósceles, si tienen dos lados iguales, y escalenos, si los tres lados son distintos. <br> | + | Según la longitud de sus lados, los triángulos se clasifican en equiláteros, si sus tres lados son iguales, isósceles, si tienen dos lados iguales, y escalenos, si los tres lados son distintos. <br> |
| − | === | + | === [[Image:Triángulo lados.jpg|thumb|center|Clasificación segñun lados]]Según sus ángulos<br> === |
| − | Si los tres ángulos son agudos el triángulo se llama acutángulo, si tiene una ángulo recto, rectángulo y obtusángulo si el mayor de sus ángulos es obtuso. <br><br><br> | + | Si los tres ángulos son agudos el triángulo se llama acutángulo, si tiene una ángulo recto, rectángulo y obtusángulo si el mayor de sus ángulos es obtuso. <br> |
| + | |||
| + | == [[Image:Triángulo ángulos.jpg|thumb|center|Clasificación según ángulos]]<br>Triángulos rectángulos == | ||
| + | |||
| + | Los triángulos rectángulos cumplen una serie de relaciones métricas importantes entre sus lados.<br>Los lados de un triángulo rectángulo que forman el ángulo recto, b y c, se llaman catetos y el tercer lado, a, (opuesto al ángulo recto) es la hipotenusa. El teorema de Pitágoras relaciona los dos catetos y la hipotenusa: en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos: a<sup>2</sup> = b<sup>2</sup> + c<sup>2</sup><br>Otra relación importante que se cumple en un triángulo rectángulo es el teorema del cateto: el cuadrado de cada cateto es igual al producto de la hipotenusa por su proyección sobre ella, es decir, c<sup>2</sup> = a • m, b<sup>2</sup> = a • n <br><br><br> | ||
| + | |||
| + | [[Category:Geometría_euclídea]] | ||
<br> | <br> | ||
Revisión del 11:45 25 jun 2010
| ||||||
Triángulo(figura): Polígono de tres lados. La suma de los tres ángulos de un triángulo es 180º. Dos de los ángulos son, necesariamente, agudos. El tercero puede ser también agudo, o bien recto u obtuso.
Sumario
Clasificación
Los triángulos se clasifican según la longitud de sus lados, o según la amplitud de sus ángulos.
Según sus lados
Según la longitud de sus lados, los triángulos se clasifican en equiláteros, si sus tres lados son iguales, isósceles, si tienen dos lados iguales, y escalenos, si los tres lados son distintos.
Según sus ángulos
Si los tres ángulos son agudos el triángulo se llama acutángulo, si tiene una ángulo recto, rectángulo y obtusángulo si el mayor de sus ángulos es obtuso.
Triángulos rectángulos
Los triángulos rectángulos cumplen una serie de relaciones métricas importantes entre sus lados.
Los lados de un triángulo rectángulo que forman el ángulo recto, b y c, se llaman catetos y el tercer lado, a, (opuesto al ángulo recto) es la hipotenusa. El teorema de Pitágoras relaciona los dos catetos y la hipotenusa: en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos: a2 = b2 + c2
Otra relación importante que se cumple en un triángulo rectángulo es el teorema del cateto: el cuadrado de cada cateto es igual al producto de la hipotenusa por su proyección sobre ella, es decir, c2 = a • m, b2 = a • n