Diferencia entre revisiones de «Grafo bipartido»
(→Definición.) |
(Página creada con '{{Definición|nombre=Grafo bipartido|imagen=k23.png|concepto=Grafo simple sin lazos de forma ''G=<V<sub>1</sub> U V<sub>2</sub>,A>'' donde ''V<sub>1</sub>'' y ''V<sub>2</sub>'' ...') |
||
| Línea 6: | Línea 6: | ||
Un grafo ''G=<V,A>'' se dice '''bipartido''' o '''bipartito''' si y solo si existe una partición de ''V=V<sub>1</sub> U V<sub>2</sub>'' tal que para toda arista ''(x,y)'' de ''A'' se cumple que ''x'' es un vertice de ''V<sub>1</sub>'' e ''y'' está en ''V<sub>2</sub>'' o simplemente que ''A'' será un subconjunto no nulo de ''V<sub>1</sub>xV<sub>2</sub>''. | Un grafo ''G=<V,A>'' se dice '''bipartido''' o '''bipartito''' si y solo si existe una partición de ''V=V<sub>1</sub> U V<sub>2</sub>'' tal que para toda arista ''(x,y)'' de ''A'' se cumple que ''x'' es un vertice de ''V<sub>1</sub>'' e ''y'' está en ''V<sub>2</sub>'' o simplemente que ''A'' será un subconjunto no nulo de ''V<sub>1</sub>xV<sub>2</sub>''. | ||
| − | Cuando ''A=V<sub>1</sub>xV<sub>2</sub>'' se dice que el grafo es [[ | + | Cuando ''A=V<sub>1</sub>xV<sub>2</sub>'' se dice que el grafo es [[bipartido completo|Knm]]. |
==Ejemplos.== | ==Ejemplos.== | ||
Revisión del 12:44 29 nov 2011
| ||||||
Grafo bipartido. Dícese de todo grafo simple sin lazos cuyo conjunto de vértices puede dividirse en dos subconjuntos disjuntos no vacíos de manera que los vértices que los componen solo tengan aristas o arcos con vértices del otro subconjunto, nunca con ningún vértice del mismo conjunto.
Definición.
Un grafo G=<V,A> se dice bipartido o bipartito si y solo si existe una partición de V=V1 U V2 tal que para toda arista (x,y) de A se cumple que x es un vertice de V1 e y está en V2 o simplemente que A será un subconjunto no nulo de V1xV2.
Cuando A=V1xV2 se dice que el grafo es Knm.
Ejemplos.
- El grafo bipartido trivial es K2.
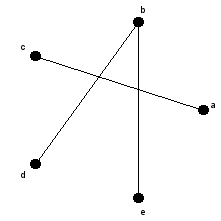
- G=<{a,b}U{c,d,e}, {(a,c),(b,d),(b,e}> es bipartito:
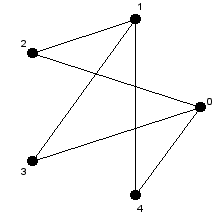
- Un de los grafos de Kuratowvski, K3,3 es bipartido.
- Todos los Kn,m son bipartidos.
Fuentes.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir. Moscú, 1988. Páginas 17-23.
- Grafo bipartito en Wikipedia.