Diferencia entre revisiones de «Modelo matemático de programación lineal»
| Línea 3: | Línea 3: | ||
|imagen= | |imagen= | ||
|tamaño= | |tamaño= | ||
| − | |concepto= Un modelo matemática de programación lineal consiste en una función objetivo y un conjunto de restricciones en la forma de un sistema de ecuaciones o inecuaciones. | + | |concepto= Un modelo matemática de [[programación lineal]] consiste en una función objetivo y un conjunto de restricciones en la forma de un sistema de ecuaciones o inecuaciones. |
}} | }} | ||
| − | + | ''' El Modelo matemático de [[programación lineal]]''' está dado por una función lineal de varias variables, en el cual se quieren determinar valores no negativos para dichas variables que maximizan o minimicen el valor de la función lineal, sujeta a cierto número de limitaciones. | |
==Formulación del modelo matemático== | ==Formulación del modelo matemático== | ||
Hallar los valores de xj que hagan máximo o mínimo el valor de la función lineal (Función objetivo). | Hallar los valores de xj que hagan máximo o mínimo el valor de la función lineal (Función objetivo). | ||
Revisión del 11:12 30 jun 2015
| ||||
El Modelo matemático de programación lineal está dado por una función lineal de varias variables, en el cual se quieren determinar valores no negativos para dichas variables que maximizan o minimicen el valor de la función lineal, sujeta a cierto número de limitaciones.
Formulación del modelo matemático
Hallar los valores de xj que hagan máximo o mínimo el valor de la función lineal (Función objetivo).
Y que satisfagan el sistema de restricciones
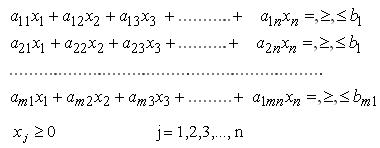
Donde para cada restricción se utiliza uno solo de los signos
xj – Variables de decisión
cj – Coeficientes económicos
aij – Coeficientes tecnológicos
bj – Termino independiente
- Variables de decisión : Incógnitas del modelo, lo que se busca con la solución del mismo. Actividades o productos que compiten por los recursos materiales, técnicos, tiempo disponible, etc.
- Coeficientes económicos : Coeficientes de la función objetivo para cada actividad o producto. Contribución de cada variable de decisión a la función objetivo, como por ejemplo, ganancia o costo por unidad de producto.
- Coeficientes tecnológicos : Coeficientes de parte izquierda de las restricciones: Representan, por ejemplo, unidades de un recurso necesarias para producir una unidad de un producto, horas de tiempo de troquelado por tipo de materiales a troquelar, horas en horno por unidad de pieza a fundir, etc.
- Términos independientes : Términos de la parte derecha de las restricciones: Representan la disponibilidad o demanda de los recursos, como por ejemplo, horas-hombre, horas-máquina, espacio, dinero, materia prima, requerimientos de calidad, capacidad de producción, cantidad máxima o mínima, etc.
Pasos para Formulación del modelo matemático
- Determinar las variables de decisión y expresarlas algebraicamente.
- Determinar las restricciones y se expresarlas como ecuaciones o inecuaciones dependientes de las variables de decisión
- Expresar todas las condiciones implícitamente establecidas por la naturaleza de las variables: que no puedan ser negativas, que sean enteras, que solo puedan tomar determinados valores, ...
- Determinar la función objetivo.
Fuente
- Charles A. G y Hugh J. W. (2005) Métodos Cuantitativos para la toma de decisiones en administración en 2 partes. Editorial Universitaria. La Habana.
- Colectivo de Autores (2013). Investigación de Operaciones. Editorial Universitaria. La Habana
- Colectivo de Autores (2013). Investigación de Operaciones. Modelos y Métodos Determinísticos. Editorial Universitaria. La Habana
- Eppen, G. D (2000). Investigación de Operaciones en la Ciencia Administrativa. Creación de modelos de decisiones con hojas de cálculo electrónicas. Prentice- Hall. México