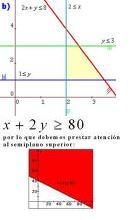
Diferencia entre revisiones de «Inecuación Lineal»

(→‎Inecuaciones lineales o inecuaciones de primer grado)
(Etiqueta: revisar proyecto)
m (Modificado el artículo (tenía muchos errores).)
Línea 4: Línea 4:
 
|concepto=Son desigualdades en las que se encuentra presente en uno, cual­quiera de los miembros, o en ambos, una o más variables, o incógnitas.
 
|concepto=Son desigualdades en las que se encuentra presente en uno, cual­quiera de los miembros, o en ambos, una o más variables, o incógnitas.
 
}}<div align=justify>
 
}}<div align=justify>
−
'''Inecuaciones lineales'''. Son desigualdades en las que interviene una variable, números y uno de los signos de desigualdad, las cuales se tornan verdaderas para determinados valores de la [[Variables|variable]].  
+
'''Inecuaciones lineales''' o '''de primer grado'''. Son desigualdades en las que interviene una o más [[incógnita|incógnitas]], números y uno de los signos de desigualdad (">", "<", "&ge;", "&le;"), las cuales se verifican para determinados valores de las incógnitas.  
  
−
== Inecuaciones lineales o inecuaciones de primer grado ==  
+
=== Ejemplos ===
 +
*La solución de la inecuación lineal x + 1 > 0 es x > -1.
 +
*La solución de la inecuación lineal x + 2 > 2x  es x < 2.
 +
<hr/>
 +
== Resolución  ==
  
−
En las inecuaciones de primer grado, el grado máximo de los [[monomio|monomios]] es 1.  
+
Para resolver una inecuación lineal con una incógnita se deben encontrar los valores de la ésta para los cuales se cumple la desigualdad. La solución de una inecuación es un intervalo. Para encontrarla, se debe simplificar la expresión polinómica del mismo modo que se realiza en las ecuaciones de primer grado, pero al dividir la inecuación por un número negativo debe cambiarse el signo de la desigualdad.  
  
−
Suponemos que ya conocemos l
+
=== Ejemplos ===
−
Ejemplos como estos se conocen como desigualdades. Una inecuación es el enunciado de una desigualdad que incluye alguna de las siguientes relaciones de orden: “mayor que”(>); “menor que” (<); “mayor o igual que” (≥), y “menor o igual que” (≤)<br />
+
*Para obtener la solución de la inecuación -2x < 4 se divide la inecuación por el número negativo -2, obteniendo x > -2.
−
En la desigualdad aparece al menos una incógnita o valor desconocido y que se cumple para ciertos valores de ella. Si el grado de la inecuación es uno (de primer grado), se dice que la inecuación es lineal. Esto porque al escribir las desigualdades usamos números y por esto mismo es que podemos usar la recta numérica para visualizar o graficar dichas desigualdades.  
+
*Para resolver la inecuación -3x +5 > 5x -3 se aíslan los monomios con parte literal a uno de los lados del signo: -3x -5x > -3 -5, para sumar los monomios: -8x > -8, y obtener el intervalo: x < 1.  
 +
<hr/>
  
−
Gráfico 1.1
+
== Representación de la solución ==
  
−
[[Image:Gráfico 1.1.JPG]]<br> Observa que en la recta de arriba:
+
Se puede representar la solución de una inecuación sobre la recta real, indicando los extremos del intervalo. Si un extremo está incluido en el intervalo (cuando los signos son "mayor o igual" o "menor o igual"), se indica con un punto opaco en la recta. Si el extremo no se incluye, se indica con un punto vacío.  
−
 
+
=== Ejemplo ===
−
4 > (–1),  porque 4 está a la derecha de –1 en la recta numérica.
+
*La representación de la solución x > 7 es
−
 
 
−
(–2) < 3, porque (–2) está a la izquierda de 3 en la recta numérica.  
 
−
 
 
−
(–3) < (–1), porque (-3) está a la izquierda de (–1) en la recta numérica
 
−
 
 
−
0 > (–4), porque 0 está a la derecha de (–4) en la recta numérica.<br />
 
−
Una inecuación lineal, entonces, es una expresión matemática que describe cómo se relacionan entre sí dos expresiones lineales.
 
−
 
 
−
Por ejemplo: 3 + 5x ≥ 18; y otro, –2(x + 3) < –9.
 
−
 
 
−
== Como resolver una inecuación  ==
 
−
 
 
−
Resolver una inecuación se deben encontrar los valores de la incógnita para los cuales se cumple la desigualdad. La solución de una inecuación es, por lo general, un intervalo o una unión de intervalos de números reales, por ello es que se puede representar haciendo uso de intervalos en la recta numérica, la cual contiene infinitos números reales.
 
−
 
 
−
Las reglas para la resolución de una inecuación son prácticamente las mismas que se emplean para la [[Resolución de ecuaciones|resolución de ecuaciones]], pero deben tenerse presentes las propiedades de las desigualdades. Se puede ilustrar la solución de una inecuación con una gráfica, utilizando la recta numérica y marcando el intervalo entre los números que dan solución a la desigualdad. Si la solución incluye algún extremo definido del intervalo, en la gráfica se representa dicho extremo con un círculo en negrita, en cambio, si la solución no incluye el extremo, lo representamos mediante un círculo en blanco.<br />
 
−
Ejemplo: x > 7 (equis es mayor que 7)
 
−
 
 
−
gráfico 1.2
 
  
 
[[Image:Gráfico 1.2.JPG]]  
 
[[Image:Gráfico 1.2.JPG]]  
  
−
<br>
+
Los valores mayores a 7 se representan a la derecha de la recta numérico y no incluyen al 7.  
−
 
+
<hr/>
−
<br>
+
== Véase también ==  
−
 
+
*[[Inecuaciones fraccionarias]]
−
Los valores mayores a 7 se representan a la derecha de la recta numérica y no incluyen al 7. En intervalo desde el punto blanco hacia el infinito a la derecha.
+
*[[Inecuación]]
−
 
+
*[[Inecuación de segundo grado]]
−
Ejemplo: x ≥ 7 (equis es mayor o igual a 7)
 
−
 
 
−
Gráfico 1.3
 
−
 
 
−
[[Image:Gráfico_1.3.JPG]]
 
−
 
 
−
<br>
 
−
 
 
−
Los valores mayores e iguales a 7 se representan a la derecha de la recta numérica e incluyen al 7. El intervalo desde el punto negro hacia el infinito a la derecha se escribe: Nótese la postura del corchete cuando incluye y cuando no incluye una cifra determinada dentro del intervalo.
 
−
 
 
−
==Resolución de inecuaciones lineales==
 
−
 
 
−
De primer grado, con una incógnita. Algunos ejemplos a continuación.<br />
 
−
Resolver la inecuación 4x - 3 > 53 (Se lee: cuatro equis menos tres es mayor que 53)<br />
 
−
Debemos colocar las letras a un lado y los números al otro lado de la desigualdad (en este caso, mayor que (">"), entonces para llevar el (–3) al otro lado de la desigualdad, le aplicamos el operador inverso (el inverso de (–3) es +3, porque la operación inversa de la resta es la suma).
 
−
 
 
−
Tendremos: 4x − 3 + 3 > 53 + 3
 
−
 
 
−
4x > 53 +3
 
−
4x > 56
 
−
 
 
−
Ahora tenemos el número 4 que está multiplicando a la variable o incógnita x, entonces lo pasaremos al otro lado de la desigualdad dividiendo (la operación inversa de la multiplicación es la división). Obteniendo:<br />
 
−
x > 56 ÷ 4
 
−
 
 
−
x > 14
 
−
 
 
−
Entonces el valor de la incógnita o variable "x" serán todos los números mayores que 14, no incluyendo al 14.
 
−
 
 
−
==Solución gráfica==  
 
−
 
 
−
Gráfico 1.4
 
−
 
 
−
[[Image:Gráfico_1.4.JPG]]
 
−
 
 
−
<br>
 
−
 
 
−
Esto significa que en la [[Recta numérica|recta numérica]], desde el número 14 (sin incluirlo) hacia la derecha todos los valores (hasta el infinito + ∞) satisfacen la inecuación o desigualdad.<br />
 
−
En el siguiente ejemplo:<br />
 
−
–11x - 5x +1 < –65x +36 <br />
 
−
Llevamos los [[Términos semejantes|términos semejantes]] a un lado de la desigualdad y los [[Términos independientes|términos independientes]] al otro lado de la desigualdad (hemos aplicado [[Operaciones inversas|operaciones inversas]] donde era necesario).<br />
 
−
–11x –5x +65x < 36 –1<br />
 
−
Resolvemos las operaciones indicadas anteriormente<br />
 
−
49x < 35<br />
 
−
Aplicando operaciones inversas queda<br />
 
−
x < 35/49<br />
 
−
De donde al simplificar resulta<br />
 
−
 
−
x < 5/7
 
−
 
 
−
== Casos especiales  ==
 
−
 
 
−
Cuando el [[Coeficiente de la variable|coeficiente de la variable]] es negativo (–), se debe tener en cuenta que al despejar la variable hay que multiplicar o dividir por un número negativo y entonces es evidente que la desigualdad se invierte.<br />
 
−
Ejemplo:<br />
 
−
2 es menor que 5, ahora multipliquemos ambos miembros de la desigualdad por (-3)<br />
 
−
¿Qué obtenemos?<br />
 
−
2 < 5 <br />
 
−
2.(-3)=(-6)<br />
 
−
5.(-3)=(-15)<br />
 
−
Se inverte el sentido de la desigualdad para que sea cierta, ya que:<br />
 
−
(-6)>(-15)<br />
 
−
En el siguiente ejemplo:<br />
 
−
2x –[x –(x –50)] < x – (800 –3x)<br />
 
−
Primero se eliminan los paréntesis<br />
 
−
2x –[x –x +50] < x –800 +3x<br />
 
−
Reducir términos semejantes.<br />
 
−
2x –[50] < 4x –800<br />
 
−
Ahora eliminar los corchetes<br />
 
−
2x –50 < 4x –800<br />
 
−
Transponer los términos, empleando el criterio de operaciones inversas.<br />
 
−
2x –4x < –800 +50<br />
 
−
Nuevamente reducir términos semejantes <br />
 
−
–2x < –750<br />
 
−
Dividir por (-2) ambos miembros y por tanto se invierte el sentido de la desigualdad obteniendo<br />
 
−
x > 750/2<br />
 
−
x > 375
 
  
−
== Fuente ==
+
== Fuentes ==
  
−
*http://www.profesorenlinea.cl/matematica/Inecuaciones_lineales.html
+
*[https://www.matesfacil.com/ESO/inecuaciones/ejercicios-resueltos-inecuaciones.html Inecuaciones resueltas de primer y segundo grado y racionales (matesfacil.com)]
−
*http://www.scribd.com/doc/.../Ecuaciones-e-inecuaciones-lineales
+
*[http://www.profesorenlinea.cl/matematica/Inecuaciones_lineales.html Inecuaciones lineales (profesorenlinea.cl)]
−
*http://recursostic.educacion.es/.../inecuaciones.../inecuaciones/inec. 
 
  
 
[[Category:Matemáticas]]
 
[[Category:Matemáticas]]

Revisión del 03:39 9 dic 2016

Inecuaciones lineales
Información sobre la plantilla
Inecuaci.JPG
Concepto:Son desigualdades en las que se encuentra presente en uno, cual­quiera de los miembros, o en ambos, una o más variables, o incógnitas.

Inecuaciones lineales o de primer grado. Son desigualdades en las que interviene una o más incógnitas, números y uno de los signos de desigualdad (">", "<", "≥", "≤"), las cuales se verifican para determinados valores de las incógnitas.

Ejemplos

  • La solución de la inecuación lineal x + 1 > 0 es x > -1.
  • La solución de la inecuación lineal x + 2 > 2x es x < 2.

Resolución

Para resolver una inecuación lineal con una incógnita se deben encontrar los valores de la ésta para los cuales se cumple la desigualdad. La solución de una inecuación es un intervalo. Para encontrarla, se debe simplificar la expresión polinómica del mismo modo que se realiza en las ecuaciones de primer grado, pero al dividir la inecuación por un número negativo debe cambiarse el signo de la desigualdad.

Ejemplos

  • Para obtener la solución de la inecuación -2x < 4 se divide la inecuación por el número negativo -2, obteniendo x > -2.
  • Para resolver la inecuación -3x +5 > 5x -3 se aíslan los monomios con parte literal a uno de los lados del signo: -3x -5x > -3 -5, para sumar los monomios: -8x > -8, y obtener el intervalo: x < 1.

Representación de la solución

Se puede representar la solución de una inecuación sobre la recta real, indicando los extremos del intervalo. Si un extremo está incluido en el intervalo (cuando los signos son "mayor o igual" o "menor o igual"), se indica con un punto opaco en la recta. Si el extremo no se incluye, se indica con un punto vacío.

Ejemplo

  • La representación de la solución x > 7 es

Gráfico 1.2.JPG

Los valores mayores a 7 se representan a la derecha de la recta numérico y no incluyen al 7.

Véase también

Fuentes

Obtenido de «https://www.ecured.cu/index.php?title=Inecuación_Lineal&oldid=2758130»