Diferencia entre revisiones de «Conexión de resistencias en serie-paralelo»
| Línea 9: | Línea 9: | ||
'''Conexión de resistencias en serie-paralelo'''. Recibe este nombre donde hay uniones de resistencias independientes tanto en [[serie]] como en [[paralelo]]. | '''Conexión de resistencias en serie-paralelo'''. Recibe este nombre donde hay uniones de resistencias independientes tanto en [[serie]] como en [[paralelo]]. | ||
==Resistencia total== | ==Resistencia total== | ||
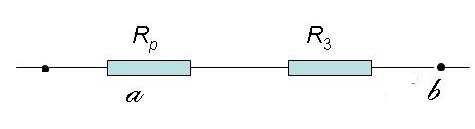
| − | Para calcular la resistencia total de este circuito, primero se calcula la resistencia equivalente a las dos en paralelo, luego nos queda un [[circuito equivalente]] | + | Para calcular la resistencia total de este circuito, primero se calcula la resistencia equivalente a las dos en paralelo, luego nos queda un [[circuito equivalente]] de la siguiente figura.<br /> |
[[Archivo:ResistenciaS_P1.jpg]] | [[Archivo:ResistenciaS_P1.jpg]] | ||
Revisión del 13:09 5 may 2017
| ||||||
Conexión de resistencias en serie-paralelo. Recibe este nombre donde hay uniones de resistencias independientes tanto en serie como en paralelo.
Resistencia total
Para calcular la resistencia total de este circuito, primero se calcula la resistencia equivalente a las dos en paralelo, luego nos queda un circuito equivalente de la siguiente figura.
Como la resistencia equivalente (Rp) que calculamos nos queda en serie con R3, se suman ambas para hallar el valor de la resistencia total.
Ejemplo
R1=3Ω, R2=6Ω y R3 = 8Ω. La tensión aplicada entre los puntos a y b es 24 V. Determinar: a) La resistencia total. b) La corriente total. c) La corriente en cada resistencia.
Solución
a) RT = Rp + R3 Archivo:SolucionS P.jpg Rp= 2Ω RT = Rp + R3 RT = 2 + 8 RT = 10 Ω
Fuentes
- Electrotecnia General. Eberto Alfonso Lastra