Velocidad lineal

Velocidad lineal. Concepto: La rapidez con que el cuerpo se desplaza desde un punto a otro de su trayectoria (el vector velocidad es perpendicular al radio)

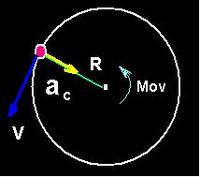
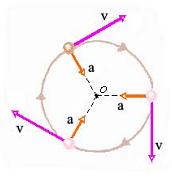
La velocidad lineal. Es aquella cuya dirección es siempre tangente a la trayectoria de la partícula que rota. Esta velocidad tiene dirección perpendicular al eje de rotación (es decir, al vector ω ) a la aceleración centrípeta y al radio vector.

Denotación

Se denota con la letra(v) y se expresa en metros/segundos (m/s)

Velocidad lineal como vector

Velocidad lineal y Aceleración centrípeta son perpendiculares entre sí

En el Movimiento circular uniforme la velocidad lineal como vector, varía en dirección y sentido, pero no en módulo, esto se debe a que la trayectoria es curvilínea, al cambiar la dirección de la velocidad cambia ésta como vector, y entonces surge una aceleración centrípeta.

Relación entre la velocida lineal y la velocidad angular

Entre la velocidad lineal, v, el radio R de la trayectoria y la velocidad angular, ω, existe la siguiente relación:

                           v= ωR

De igual manera, entre la velocidad lineal y la aceleración centrípeta existe la siguiente relación:

                          a= v²/R 

Velocidad lineal y el radio como vectores

Velocidad lineal y el radio vector, son perpendiculares entre sí

Fuentes

• Sears-Zemansky (Volumen1), página 288. Física Universitaria. ISBN 978-607-442-288-7
• Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons. ISBN 0-471-32057-9.
• Velocidad angular del planeta Tierra, Consultado de la Red C.U.B.A el 29 de Junio de 2017
• Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons. ISBN 0-471-32057-9.
• Lic José Manuel Mora Hernández.Documento digital:Centro nacional de entrenamientos para las Olimpiadas, página 30.
• Velocidad lineal
• B.M.Yavorski-A.A.Detlaf. Prontuario de Física, página 27 (traducido del ruso por el ingeniero Antonio Molina García)

Categorías: