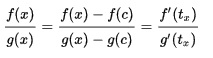Diferencia entre revisiones de «Regla de l'Hôpital»
(Página creada con «{{Desarrollo}} {{Definición|Nombre= Regla de l'Hôpital |imagen= |concepto= }} <div align="justify">''' Regla de l'Hôpital.''' Guillaume de l'Hôpital, fue el que dio a...») |
|||
| Línea 4: | Línea 4: | ||
<div align="justify">''' Regla de l'Hôpital.''' Guillaume de l'Hôpital, fue el que dio a conocer esta regla.En matemática, más específicamente en el cálculo diferencial, la regla de l'Hôpital o regla de l'Hôpital-Bernoulli1 es una regla que usa derivadas para ayudar a evaluar límites de funciones que estén en forma indeterminada. Esta regla recibe su nombre en honor al matemático francés del siglo XVII Guillaume François Antoine, marqués de l'Hôpital (1661 - 1704), quien dio a conocer la regla en su obra Analyse des infiniment petits pour l'intelligence des lignes courbes (1696), el primer texto que se ha escrito sobre cálculo diferencial, aunque actualmente se sabe que la regla se debe a Johann Bernoulli, que fue quien la desarrolló y demostró.1 La explicación es que ambos habían entrado en un curioso arreglo de negocios por medio del cual el marqués de L'Hopital compró los derechos de los descubrimientos matemáticos de Bernoulli.3 | <div align="justify">''' Regla de l'Hôpital.''' Guillaume de l'Hôpital, fue el que dio a conocer esta regla.En matemática, más específicamente en el cálculo diferencial, la regla de l'Hôpital o regla de l'Hôpital-Bernoulli1 es una regla que usa derivadas para ayudar a evaluar límites de funciones que estén en forma indeterminada. Esta regla recibe su nombre en honor al matemático francés del siglo XVII Guillaume François Antoine, marqués de l'Hôpital (1661 - 1704), quien dio a conocer la regla en su obra Analyse des infiniment petits pour l'intelligence des lignes courbes (1696), el primer texto que se ha escrito sobre cálculo diferencial, aunque actualmente se sabe que la regla se debe a Johann Bernoulli, que fue quien la desarrolló y demostró.1 La explicación es que ambos habían entrado en un curioso arreglo de negocios por medio del cual el marqués de L'Hopital compró los derechos de los descubrimientos matemáticos de Bernoulli.3 | ||
==Enunciado== | ==Enunciado== | ||
| − | La regla de L'Hôpital es una consecuencia del Teorema del valor medio de Cauchy que se da sólo en el caso de las indeterminaciones del tipo | + | La regla de L'Hôpital es una consecuencia del Teorema del valor medio de Cauchy que se da sólo en el caso de las indeterminaciones del tipo |
| + | <div align="left">''' [[Archivo:l´hospital-1.jpg]] | ||
Sean f y g dos funciones continuas definidas en el intervalo [a,b], derivables en (a,b) y sea c perteneciente a (a,b) tal que f(c)=g(c)=0 y g'(x)≠0 si x≠c. | Sean f y g dos funciones continuas definidas en el intervalo [a,b], derivables en (a,b) y sea c perteneciente a (a,b) tal que f(c)=g(c)=0 y g'(x)≠0 si x≠c. | ||
| − | Si existe el límite L de f'/g' en c, entonces existe el límite de f/g (en c) y es igual a L. Por | + | Si existe el límite L de f'/g' en c, entonces existe el límite de f/g (en c) y es igual a L. Por lo tanto: |
| + | <div align="left">''' [[Archivo:l´hospital-2.jpg]] | ||
==Demostración== | ==Demostración== | ||
| − | El siguiente argumento se puede tomar como una «demostración» de la regla de L'Hôpital, aunque en realidad, una demostración rigurosa requiere de argumentos de tipo Ɛ- | + | El siguiente argumento se puede tomar como una «demostración» de la regla de L'Hôpital, aunque en realidad, una demostración rigurosa requiere de argumentos de tipo Ɛ-δ más delicados. |
*Como g(c) = 0 y g'(x) ≠ 0 si x ≠ c , se tiene que si g(x)≠0 si x ≠ c como consecuencia del Teorema de Rolle. | *Como g(c) = 0 y g'(x) ≠ 0 si x ≠ c , se tiene que si g(x)≠0 si x ≠ c como consecuencia del Teorema de Rolle. | ||
| − | *Dado que f(c)=g(c)=0, aplicando el Teorema del Valor Medio de Cauchy, para todo x en (a,b), con x distinto de c, existe tx en el intervalo de extremos a y b, tal que el cociente f(x)/g(x) se puede escribir de la siguiente manera: | + | *Dado que f(c)=g(c)=0, aplicando el Teorema del Valor Medio de Cauchy, para todo x en (a,b), con x distinto de c, existe tx en el intervalo de extremos a y b, tal que el cociente f(x)/g(x) se puede escribir de la siguiente manera:<div align="left">''' [[Archivo:l´hospital-3.jpg]] |
| − | *Cuando x tiende hacia c, igualando los valores de las igualdades de arriba, tx también tiende hacia c, así que | + | *Cuando x tiende hacia c, igualando los valores de las igualdades de arriba, tx también tiende hacia c, así que |
| + | <div align="left">''' [[Archivo:l´hospital-4.jpg]] | ||
Nota: el último paso al límite, aunque es cierto, requeriría una justificación más rigurosa. | Nota: el último paso al límite, aunque es cierto, requeriría una justificación más rigurosa. | ||
| Línea 22: | Línea 25: | ||
===Aplicación sencilla=== | ===Aplicación sencilla=== | ||
| − | + | <div align="left">''' [[Archivo:l´hospital-5.jpg]] | |
===Aplicación consecutiva=== | ===Aplicación consecutiva=== | ||
Mientras la función sea n veces continua y derivable, la regla puede aplicarse n veces: | Mientras la función sea n veces continua y derivable, la regla puede aplicarse n veces: | ||
| − | [[Archivo:l´hospital-6.jpg | + | <div align="left">''' [[Archivo:l´hospital-6.jpg]] |
===Adaptaciones algebraicas=== | ===Adaptaciones algebraicas=== | ||
| Línea 33: | Línea 36: | ||
===Cocientes incompatibles=== | ===Cocientes incompatibles=== | ||
Las indeterminaciones de tipo ∞/∞ se pueden transformar mediante la doble inversión de los cocientes: | Las indeterminaciones de tipo ∞/∞ se pueden transformar mediante la doble inversión de los cocientes: | ||
| − | + | <div align="left">''' [[Archivo:l´hospital-7.jpg]] | |
| Línea 40: | Línea 43: | ||
| − | A veces algunos límites indeterminados que no se presentan como cocientes pueden ser resueltos con esta regla, recurriendo a transformaciones previas que lleven a un cociente del tipo | + | A veces algunos límites indeterminados que no se presentan como cocientes pueden ser resueltos con esta regla, recurriendo a transformaciones previas que lleven a un cociente del tipo <div align="left">''' [[Archivo:l´hospital-8.jpg]] |
| − | + | *Tipo 0 ∙ ∞ | |
| − | Se trata de hacer una transformación como: | + | Se trata de hacer una transformación como: <div align="left">''' [[Archivo:l´hospital-9.jpg]] |
| − | + | *El más clásico: <div align="left">''' [[Archivo:l´hospital-10.jpg]] | |
==Generalizaciones== | ==Generalizaciones== | ||
| − | + | *La regla de L'Hôpital vale para límites laterales, límites en el infinito y límites infinitos. | |
| − | + | *La regla de L'Hôpital se puede extender a funciones escalares de n variables que sean diferenciables. Dadas dos funciones diferenciables f y g tales que f(c) = g(c) = 0, se tiene: | |
| − | + | <div align="left">''' [[Archivo:L´hospital-11.jpg]] | |
| − | + | ,representan los gradientes de ambas funciones escalares. | |
| − | a•b | + | a•b,representa el producto escalar de dos vectores. |
| − | ‖•‖ | + | ‖•‖,representa la norma de un vector. |
| − | + | ,es el ángulo formado por el gradiente de f y el vector x-c. | |
| − | + | ,es el ángulo formado por el gradiente de g y el vector x-c. | |
| − | |||
==Fuentes== | ==Fuentes== | ||
Revisión del 18:07 26 sep 2017
| ||
Regla de l'Hôpital. Guillaume de l'Hôpital, fue el que dio a conocer esta regla.En matemática, más específicamente en el cálculo diferencial, la regla de l'Hôpital o regla de l'Hôpital-Bernoulli1 es una regla que usa derivadas para ayudar a evaluar límites de funciones que estén en forma indeterminada. Esta regla recibe su nombre en honor al matemático francés del siglo XVII Guillaume François Antoine, marqués de l'Hôpital (1661 - 1704), quien dio a conocer la regla en su obra Analyse des infiniment petits pour l'intelligence des lignes courbes (1696), el primer texto que se ha escrito sobre cálculo diferencial, aunque actualmente se sabe que la regla se debe a Johann Bernoulli, que fue quien la desarrolló y demostró.1 La explicación es que ambos habían entrado en un curioso arreglo de negocios por medio del cual el marqués de L'Hopital compró los derechos de los descubrimientos matemáticos de Bernoulli.3
Sumario
Enunciado
La regla de L'Hôpital es una consecuencia del Teorema del valor medio de Cauchy que se da sólo en el caso de las indeterminaciones del tipo
Archivo:L´hospital-1.jpg
Sean f y g dos funciones continuas definidas en el intervalo [a,b], derivables en (a,b) y sea c perteneciente a (a,b) tal que f(c)=g(c)=0 y g'(x)≠0 si x≠c. Si existe el límite L de f'/g' en c, entonces existe el límite de f/g (en c) y es igual a L. Por lo tanto:
Demostración
El siguiente argumento se puede tomar como una «demostración» de la regla de L'Hôpital, aunque en realidad, una demostración rigurosa requiere de argumentos de tipo Ɛ-δ más delicados.
- Como g(c) = 0 y g'(x) ≠ 0 si x ≠ c , se tiene que si g(x)≠0 si x ≠ c como consecuencia del Teorema de Rolle.
- Dado que f(c)=g(c)=0, aplicando el Teorema del Valor Medio de Cauchy, para todo x en (a,b), con x distinto de c, existe tx en el intervalo de extremos a y b, tal que el cociente f(x)/g(x) se puede escribir de la siguiente manera:
- Cuando x tiende hacia c, igualando los valores de las igualdades de arriba, tx también tiende hacia c, así que
Nota: el último paso al límite, aunque es cierto, requeriría una justificación más rigurosa.
Ejemplos
La regla de l'Hôpital se aplica para salvar indeterminaciones que resultan de reemplazar el valor numérico al llevar al límite las funciones dadas. La regla dice que, se deriva el numerador y el denominador, por separado; es decir: sean las funciones originales f(x)/g(x), al aplicar la regla se obtendrá: f'(x)/g'(x).
Aplicación sencilla
Aplicación consecutiva
Mientras la función sea n veces continua y derivable, la regla puede aplicarse n veces:
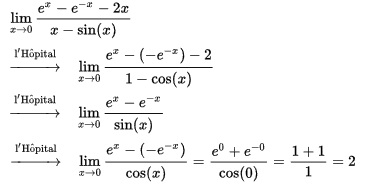
Adaptaciones algebraicas
Dada la utilidad de la regla, resulta práctico transformar otros tipos de indeterminaciones al tipo 0/0mediante transformaciones algebraicas:
Cocientes incompatibles
Las indeterminaciones de tipo ∞/∞ se pueden transformar mediante la doble inversión de los cocientes:
De esta forma se puede demostrar que las indeterminaciones de tipo ∞/∞ también se pueden resolver por medio de la aplicación de la regla de L'Hôpital de forma directa, sin aplicación de la doble inversión.
Indeterminaciones no cocientes
A veces algunos límites indeterminados que no se presentan como cocientes pueden ser resueltos con esta regla, recurriendo a transformaciones previas que lleven a un cociente del tipo
- Tipo 0 ∙ ∞
- El más clásico:
Generalizaciones
- La regla de L'Hôpital vale para límites laterales, límites en el infinito y límites infinitos.
- La regla de L'Hôpital se puede extender a funciones escalares de n variables que sean diferenciables. Dadas dos funciones diferenciables f y g tales que f(c) = g(c) = 0, se tiene:
Archivo:L´hospital-11.jpg
,representan los gradientes de ambas funciones escalares. a•b,representa el producto escalar de dos vectores. ‖•‖,representa la norma de un vector. ,es el ángulo formado por el gradiente de f y el vector x-c. ,es el ángulo formado por el gradiente de g y el vector x-c.
Fuentes
• Stewart, James (2004). Calculus : concepts and contexts (3rd ed. edición). Belmont, CA: Thomson Brooks/Cole. p. 298. ISBN 0-534-40986-5. • Howard Eves, in mathematic al Circles (Volumen 2: Cuadrantes III y IV)(Boston: Prindle, Weber and Schmidt,1969), pp. 20-22
