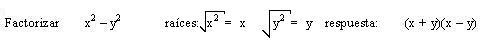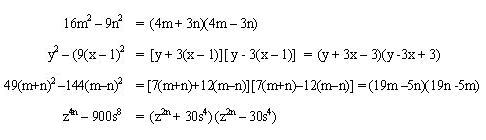Diferencia entre revisiones de «Diferencia de cuadrados»
(Etiquetas: nuestro-nuestra, revisar proyecto) |
(Etiquetas: nuestro-nuestra, revisar proyecto) |
||
| Línea 47: | Línea 47: | ||
<u>Del ejemplo anterior son términos: </u> | <u>Del ejemplo anterior son términos: </u> | ||
| − | + | ||
| + | 5abx; 258bx; -36ay | ||
<u>Otros términos son:</u> | <u>Otros términos son:</u> | ||
| − | + | ||
| + | -4k; 3x/4mn; 5/3√y | ||
<u>Todos los términos poseen un signo, un coeficiente y una parte literal, así:</u> | <u>Todos los términos poseen un signo, un coeficiente y una parte literal, así:</u> | ||
| − | Término | + | Término Signo Coeficiente Literal |
| − | + | -59ax - 59 ax | |
| − | + | 8v³ + 8 v³ | |
| − | + | xyz + 1 xyz | |
| − | + | -89 - 89 | |
== Diferencia de cuadrados – Álgebra == | == Diferencia de cuadrados – Álgebra == | ||
Revisión del 02:01 5 dic 2018
| ||
Sumario
Introducción
Se trabaja con las mismas reglas que en la aritmética agregando un par de conceptos tales como las formulas y las ecuaciones. En el Álgebra se estudia los números de el modo mas general posible.
En el álgebra los números son representados por símbolos tales como a,b,x,y
En el álgebra se usan letras para representar números o usamos letras para la demostración de reglas y formulas para mostrarlo de una manera general que es apta para cualquier numero lo que hace de estas reglas generales para cualquier numero existente. Al usar letras para estas formulas estamos hablando en lenguaje algebraico o notación algebraica.
Símbolos algebraicos básicos:
Suma +
Resta -
Multiplicación (x), (•) ,
División ÷, /
Radicación √
Agrupación ( ), { }, [ ], ¯
Es igual a =
Es mayor que >
Es menor que <
Es mayor o igual que ≥
Es menor o igual que ≤
En el caso de la multiplicación cuando dos letras se asume que se está multiplicando así si tenemos “ab” estamos diciendo que “a” está multiplicando a “b”, o en paréntesis (a)(b) también es “a” por “b”. Y la división se puede expresar como una fracción a/b. En general una combinación de símbolos y signos del álgebra representa a un número y se llama una expresión algebraica.
Ejemplo:
5abx + 258bx – 36ay
La parte de la expresión algebraica que no se encuentra separada por un signo de suma o resta se llama término
Del ejemplo anterior son términos:
5abx; 258bx; -36ay
Otros términos son:
-4k; 3x/4mn; 5/3√y
Todos los términos poseen un signo, un coeficiente y una parte literal, así:
Término Signo Coeficiente Literal -59ax - 59 ax 8v³ + 8 v³ xyz + 1 xyz -89 - 89
Diferencia de cuadrados – Álgebra
La diferencia de cuadrados es una práctica que necesitamos tener clara para seguir avanzando en nuestro curso de Álgebra. Lo primero de todo es entender el concepto, saber qué significa la diferencia de cuadrados y cómo podemos ponerla en práctica. Por lo tanto, empecemos por el principio, la definición de diferencia de cuadrados.
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
Al estudiar los productos notables teníamos que:
En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario:
Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases. Pasos a seguir para calcula la diferencia de cuadrados:
- Se extrae la raíz cuadrada de ambos términos.
- Se multiplica la suma por la diferencia de estas cantidades (el segundo término del binomio negativo es la raíz del término del binomio que es negativo).
Factorización de una diferencia de cuadrados
La factorización de una diferencia de cuadrados está formada por una ecuación con dos términos: uno positivo y el otro, negativo. Ambos deben de ser raíces cuadradas exactas. Y lo que se hace es realizar una resta entre ellos. De ahí el nombre de factorización por diferencia de cuadrados.
Ejemplos de diferencias de cuadrados
¿Tienes claro ya qué es una diferencia de cuadrados? ¡Te dejamos aquí otros ejemplos para que lo tengas más claro!
Recuerda que tanto la diferencia de cuadrados como la factorización por diferencia de cuadrados te serán de gran utilidad para resolver problemas matemáticos y de álgebra en concreto. ¡No pases a la siguiente lección hasta que tengas claro este concepto! Solo así podrás ir aprendiendo paso a paso.
Fuentes
https://www.aulafacil.com/cursos/matematicas/algebra/diferencia-de-cuadrados-l10954