Diferencia entre revisiones de «Árbol binario»
| Línea 18: | Línea 18: | ||
*Los nodos del árbol binario serán representados como registros que contendrán como mínimo tres campos. En un campo se almacenará la información del nodo. Los dos restantes se utilizarán para apuntar al subarbol izquierdo y derecho del subarbol en cuestión. | *Los nodos del árbol binario serán representados como registros que contendrán como mínimo tres campos. En un campo se almacenará la información del nodo. Los dos restantes se utilizarán para apuntar al subarbol izquierdo y derecho del subarbol en cuestión. | ||
| − | == | + | ==Algoritmo de creación== |
Procedimiento crear (q:nodo) | Procedimiento crear (q:nodo) | ||
*inicio | *inicio | ||
| Línea 51: | Línea 51: | ||
*A. B. Completos. | *A. B. Completos. | ||
| − | ==A. B. distinto== | + | ===A. B. distinto=== |
Se dice que dos árboles binarios son distintos cuando sus estructuras son diferentes. | Se dice que dos árboles binarios son distintos cuando sus estructuras son diferentes. | ||
| Línea 57: | Línea 57: | ||
[[Archivo:Extructura_diferente.jpg]] | [[Archivo:Extructura_diferente.jpg]] | ||
| − | ==A. B. similares== | + | ===A. B. similares=== |
Dos árboles binarios son similares cuando sus estructuras son idénticas, pero la información que contienen sus nodos es diferente. | Dos árboles binarios son similares cuando sus estructuras son idénticas, pero la información que contienen sus nodos es diferente. | ||
| Línea 63: | Línea 63: | ||
[[Archivo:Similar.jpg]] | [[Archivo:Similar.jpg]] | ||
| − | ==A. B. equibalentes== | + | ===A. B. equibalentes=== |
Son aquellos árboles que son similares y que además los nodos contienen la misma información. | Son aquellos árboles que son similares y que además los nodos contienen la misma información. | ||
| Línea 70: | Línea 70: | ||
[[Archivo:Equivalente_.jpg]] | [[Archivo:Equivalente_.jpg]] | ||
| − | ==A. B.completos== | + | ===A. B.completos=== |
Son aquellos árboles en los que todos sus nodos excepto los del ultimo nivel, tiene dos hijos; el subárbol izquierdo y el subárbol derecho. | Son aquellos árboles en los que todos sus nodos excepto los del ultimo nivel, tiene dos hijos; el subárbol izquierdo y el subárbol derecho. | ||
| − | ==Recorrido de un | + | |
| + | ==Recorrido de un árbol binario== | ||
Hay tres maneras de recorrer un árbol: en inorden, preorden y postorden. Cada una de ellas tiene una secuencia distinta para analizar el árbol como se puede ver a continuación: | Hay tres maneras de recorrer un árbol: en inorden, preorden y postorden. Cada una de ellas tiene una secuencia distinta para analizar el árbol como se puede ver a continuación: | ||
| − | ==Inorden== | + | |
| + | ===Inorden=== | ||
*Recorrer el subarbol izquierdo en inorden. | *Recorrer el subarbol izquierdo en inorden. | ||
*Examinar la raíz. | *Examinar la raíz. | ||
*Recorrer el subarbol derecho en inorden. | *Recorrer el subarbol derecho en inorden. | ||
| − | ==Preorden== | + | ===Preorden=== |
*Examinar la raíz. | *Examinar la raíz. | ||
*Recorrer el subarbol izquierdo en preorden. | *Recorrer el subarbol izquierdo en preorden. | ||
*recorrer el subarbol derecho en preorden. | *recorrer el subarbol derecho en preorden. | ||
| − | ==Posorden== | + | ===Posorden=== |
*Recorrer el subarbol izquierdo en postorden. | *Recorrer el subarbol izquierdo en postorden. | ||
*Recorrer el subarbol derecho en postorden. | *Recorrer el subarbol derecho en postorden. | ||
| Línea 94: | Línea 96: | ||
*Postorden: GDHIEBKJFCA | *Postorden: GDHIEBKJFCA | ||
| − | ==Arboles | + | ==Arboles enhebrados== |
Existe un tipo especial de árbol binario llamado enhebrado, el cual contiene hebras que pueden estar a la derecha o a la izquierda. El siguiente ejemplo es un árbol binario enhebrado a la derecha. | Existe un tipo especial de árbol binario llamado enhebrado, el cual contiene hebras que pueden estar a la derecha o a la izquierda. El siguiente ejemplo es un árbol binario enhebrado a la derecha. | ||
[[Archivo:Enhebrados.jpg]] | [[Archivo:Enhebrados.jpg]] | ||
| − | * | + | *Árbol enhebrado a la derecha. Este tipo de árbol tiene un apuntador a la derecha que apunta a un nodo antecesor. |
| − | * | + | *Árbol enhebrado a la izquierda. Estos arboles tienen un apuntador a la izquierda que apunta al nodo antecesor en orden. |
| − | ==Árboles en | + | ==Árboles en montón== |
Esta sección consiste en transformar un bosque en un árbol binario. Entenderemos como bosque a un conjunto normalmente ordenado de dos o más árboles generales. | Esta sección consiste en transformar un bosque en un árbol binario. Entenderemos como bosque a un conjunto normalmente ordenado de dos o más árboles generales. | ||
| + | |||
La serie de pasos que debemos seguir para lograr la conversión de un bosque en un árbol binario es la siguiente: | La serie de pasos que debemos seguir para lograr la conversión de un bosque en un árbol binario es la siguiente: | ||
*Enlazar horizontalmente las raíces de los distintos árboles generales. | *Enlazar horizontalmente las raíces de los distintos árboles generales. | ||
| Línea 111: | Línea 114: | ||
==Fuente== | ==Fuente== | ||
| − | *[https://www.monografias.com/trabajos92/arboles-binario/arboles-binario.shtml] | + | *Arboles binarios. Disponible en: [https://www.monografias.com/trabajos92/arboles-binario/arboles-binario.shtml/ www.monografias.com] |
| − | *[https://www.utm.mx/~rruiz/cursos/ED/material/ABB.pdf] | + | *Arboles binarios. Disponible en: [https://www.utm.mx/~rruiz/cursos/ED/material/ABB.pdf/ www.utm.mx] |
| − | |||
*[https://es.wikipedia.org/wiki/Árbol_binario/ es.wikipedia.org]. | *[https://es.wikipedia.org/wiki/Árbol_binario/ es.wikipedia.org]. | ||
| + | |||
[[Category:Informática]] | [[Category:Informática]] | ||
última versión al 07:20 23 oct 2019
| ||||||
Árbol binario. A los arboles ordenados de grado dos se les conoce como arboles binarios ya que cada nodo del árbol no tendrá más de dos descendientes directos. Las aplicaciones de los arboles binarios son muy variadas ya que se les puede utilizar para representar una estructura en la cual es posible tomar decisiones con dos opciones en distintos puntos.
La representación gráfica de un árbol binario es la siguiente:
Sumario
Representación en memoria
Hay dos formas tradicionales de representar un árbol binario en memoria:
- Por medio de datos tipo punteros también conocidos como variables dinámicas o listas.
- Por medio de arreglos.
- Sin embargo la más utilizada es la primera, puesto que es la más natural para tratar este tipo de estructuras.
- Los nodos del árbol binario serán representados como registros que contendrán como mínimo tres campos. En un campo se almacenará la información del nodo. Los dos restantes se utilizarán para apuntar al subarbol izquierdo y derecho del subarbol en cuestión.
Algoritmo de creación
Procedimiento crear (q:nodo)
- inicio
- mensaje("Rama izquierda?")
- lee(respuesta)
- si respuesta = "si" entonces
- new(p)
- q(li) <-- nil
- crear(p)
- en caso contrario
- q(li) <-- nil
- mensaje("Rama derecha?")
- lee(respuesta)
- si respuesta="si" entonces
- new(p)
- q(ld)<--p
- crear(p)
- en caso contrario
- q(ld) <--nil
- fin
- INICIO
- new(p)
- raiz<--p
- crear(p)
- FIN
Clasificación
Existen cuatro tipos de árbol binario:.
- A. B. Distinto.
- A. B. Similares.
- A. B. Equivalentes.
- A. B. Completos.
A. B. distinto
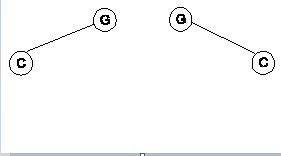
Se dice que dos árboles binarios son distintos cuando sus estructuras son diferentes.
Ejemplo:
A. B. similares
Dos árboles binarios son similares cuando sus estructuras son idénticas, pero la información que contienen sus nodos es diferente.
Ejemplo:
A. B. equibalentes
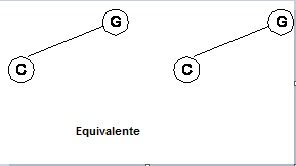
Son aquellos árboles que son similares y que además los nodos contienen la misma información.
Ejemplo:
A. B.completos
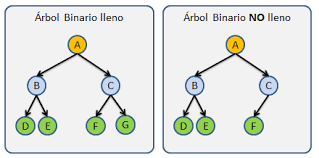
Son aquellos árboles en los que todos sus nodos excepto los del ultimo nivel, tiene dos hijos; el subárbol izquierdo y el subárbol derecho.
Recorrido de un árbol binario
Hay tres maneras de recorrer un árbol: en inorden, preorden y postorden. Cada una de ellas tiene una secuencia distinta para analizar el árbol como se puede ver a continuación:
Inorden
- Recorrer el subarbol izquierdo en inorden.
- Examinar la raíz.
- Recorrer el subarbol derecho en inorden.
Preorden
- Examinar la raíz.
- Recorrer el subarbol izquierdo en preorden.
- recorrer el subarbol derecho en preorden.
Posorden
- Recorrer el subarbol izquierdo en postorden.
- Recorrer el subarbol derecho en postorden.
- Examinar la raíz.
Ejemplo de los diferentes recorridos en un árbol binario.
- Inorden: GDBHEIACJKF
- Preorden: ABDGEHICFJK
- Postorden: GDHIEBKJFCA
Arboles enhebrados
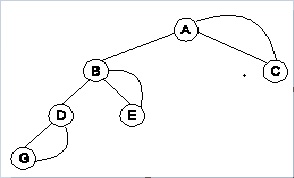
Existe un tipo especial de árbol binario llamado enhebrado, el cual contiene hebras que pueden estar a la derecha o a la izquierda. El siguiente ejemplo es un árbol binario enhebrado a la derecha.
- Árbol enhebrado a la derecha. Este tipo de árbol tiene un apuntador a la derecha que apunta a un nodo antecesor.
- Árbol enhebrado a la izquierda. Estos arboles tienen un apuntador a la izquierda que apunta al nodo antecesor en orden.
Árboles en montón
Esta sección consiste en transformar un bosque en un árbol binario. Entenderemos como bosque a un conjunto normalmente ordenado de dos o más árboles generales.
La serie de pasos que debemos seguir para lograr la conversión de un bosque en un árbol binario es la siguiente:
- Enlazar horizontalmente las raíces de los distintos árboles generales.
- Enlazar los hijos de cada nodo en forma horizontal (los hermanos).
- Enlazar verticalmente el nodo padre con el hijo que se encuentra más a la izquierda. Además debe eliminarse el vínculo de ese padre con el resto de sus hijos.
- Debe rotarse el diagrama resultante aproximadamente 45 grados hacia la izquierda y así se obtendrá el árbol binario correspondiente.
Fuente
- Arboles binarios. Disponible en: www.monografias.com
- Arboles binarios. Disponible en: www.utm.mx