Diferencia entre revisiones de «Rectas oblicuas»
(Página creada con '{{Definición |nombre=Recta Oblicua |imagen=Geometria-090-rectas-oblicuas.png |tamaño= |concepto=Si dos rectas tienen un punto de intersección, y forman ángulos no todos igua...') |
|||
| Línea 4: | Línea 4: | ||
|tamaño= | |tamaño= | ||
|concepto=Si dos rectas tienen un punto de intersección, y forman ángulos no todos iguales, las rectas se llaman oblicuas. | |concepto=Si dos rectas tienen un punto de intersección, y forman ángulos no todos iguales, las rectas se llaman oblicuas. | ||
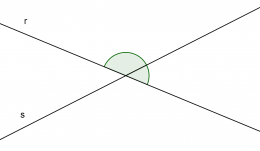
| − | }} | + | }}'''Recta Oblícua''' es cuando se cruzan en forma inclinada entre ellas, y por lo tanto dividen el plano en cuatro sectores de los cuales dos son iguales, pero distintos de los otros dos que a su vez son iguales entre sí. Es decir que forma con otra línea un ángulo que no es recto |
| − | ==Recta== | + | |
| − | [[Recta]] La línea es aquella que representa un conjunto de puntos. Una idea de recta nos la da un hilo extendido, o bien, el borde de una regla. Toda recta es limitada, las flechas indican que la recta se prolonga indefinidamente en ambos sentidos. Para referirnos a una recta (notación) se pueden seleccionar dos de sus puntos a los que se asocian letras mayúsculas. | + | == Recta == |
| − | ==Definiciones de rectas oblicuas== | + | |
| − | *Toda recta que corta a una recta formando un ángulo que no es recto, se dice que es oblicua a la recta. | + | [[Recta]] La línea es aquella que representa un conjunto de puntos. Una idea de recta nos la da un hilo extendido, o bien, el borde de una regla. Toda recta es limitada, las flechas indican que la recta se prolonga indefinidamente en ambos sentidos. Para referirnos a una recta (notación) se pueden seleccionar dos de sus puntos a los que se asocian letras mayúsculas. |
| − | *Que no es perpendicular ni paralelo a un plano, a una recta, o a una dirección determinada. | + | |
| + | == Definiciones de rectas oblicuas == | ||
| + | |||
| + | *Toda recta que corta a una recta formando un ángulo que no es recto, se dice que es oblicua a la recta. | ||
| + | *Que no es perpendicular ni paralelo a un plano, a una recta, o a una dirección determinada. | ||
*Si dos rectas tienen un punto de intersección, y forman ángulos no todos iguales, las rectas se llaman oblicuas. | *Si dos rectas tienen un punto de intersección, y forman ángulos no todos iguales, las rectas se llaman oblicuas. | ||
| − | ==Clases de rectas en un plano== | + | == Clases de rectas en un plano == |
| − | Dos rectas | + | |
| − | *Dos rectas ubicadas en el mismo plano se denominan [[Rectas Paralelas]] | + | Dos rectas o más pueden encontrarse entre sí en distintas posiciones posibles: |
| − | *Dos rectas ubicadas en el mismo plano se denominan divergentes | + | |
| − | *Dos rectas ubicadas en el mismo plano se denominan convergentes | + | *Dos rectas ubicadas en el mismo plano se denominan [[Rectas Paralelas]] cuando todos los puntos de ambas se encuentran a la misma distancia. |
| − | Es fácil advertir que en los dos últimos casos, en realidad se está haciendo referencia a semirrectas; por cuanto las divergentes resultan convergentes si se invierte el sentido de la comparación de sus distancias, y las convergentes, luego de cruzarse, se tornan divergentes. | + | *Dos rectas ubicadas en el mismo plano se denominan divergentes cuando los puntos de ambas van aumentando su distancia. |
| − | ==Clases de rectas convergentes== | + | *Dos rectas ubicadas en el mismo plano se denominan convergentes cuando los puntos de ambas van dismuyendo su distancia; y eventualmente ambas rectas se cruzan en un punto. |
| − | Las rectas convergentes, pueden ser: | + | |
| − | *[[Rectas Perpendiculares ]]: cuando dividen el plano en cuatro partes iguales; es decir, cuando al cruzarse ninguna resulta estar inclinada respecto de la otra. | + | Es fácil advertir que en los dos últimos casos, en realidad se está haciendo referencia a semirrectas; por cuanto las divergentes resultan convergentes si se invierte el sentido de la comparación de sus distancias, y las convergentes, luego de cruzarse, se tornan divergentes. |
| − | *Rectas Oblicuas :cuando se cruzan en forma inclinada entre ellas, y por lo tanto dividen el plano en cuatro sectores de los cuales dos son iguales, pero distintos de los otros dos que a su vez son iguales entre sí. | + | |
| + | == Clases de rectas convergentes == | ||
| + | |||
| + | Las rectas convergentes, pueden ser: | ||
| + | |||
| + | *[[Rectas Perpendiculares]]: cuando dividen el plano en cuatro partes iguales; es decir, cuando al cruzarse ninguna resulta estar inclinada respecto de la otra. | ||
| + | *Rectas Oblicuas :cuando se cruzan en forma inclinada entre ellas, y por lo tanto dividen el plano en cuatro sectores de los cuales dos son iguales, pero distintos de los otros dos que a su vez son iguales entre sí. | ||
| + | |||
Podemos nombrar tres posiciones si hablamos de la relación que se haya entre dos líneas rectas; éstas pueden ser paralelas, perpendiculares, u oblicuas, entre sí. Dos líneas paralelas siempre permanecen equidistantes, lo que significa que se hayan entre sí a la misma distancia en todos sus puntos; además, no se cruzan nunca. Una línea recta es perpendicular a otra cuando la corta formando ángulos de 90º. | Podemos nombrar tres posiciones si hablamos de la relación que se haya entre dos líneas rectas; éstas pueden ser paralelas, perpendiculares, u oblicuas, entre sí. Dos líneas paralelas siempre permanecen equidistantes, lo que significa que se hayan entre sí a la misma distancia en todos sus puntos; además, no se cruzan nunca. Una línea recta es perpendicular a otra cuando la corta formando ángulos de 90º. | ||
| − | ==Propiedades de rectas oblicuas== | + | |
| + | == Propiedades de rectas oblicuas == | ||
| + | |||
Rectas oblicuas. | Rectas oblicuas. | ||
| − | Si desde un punto exterior a una recta se traza la perpendicular y varias oblicuas: | + | Si desde un punto exterior a una recta se traza la perpendicular y varias oblicuas: |
*La perpendicular es menor que cualquier oblicua. | *La perpendicular es menor que cualquier oblicua. | ||
| Línea 32: | Línea 45: | ||
*Si dos oblicuas tiene diferente medida del pie de la perpendicular, es mayor la que más se aparta. | *Si dos oblicuas tiene diferente medida del pie de la perpendicular, es mayor la que más se aparta. | ||
| − | Las líneas rectas oblicuas se originan en puntos diferentes, pero luego se cruzan, dando lugar a ángulos agudos y obtusos (nunca rectos). | + | Las líneas rectas oblicuas se originan en puntos diferentes, pero luego se cruzan, dando lugar a ángulos agudos y obtusos (nunca rectos). |
| + | |||
| + | == Enlace externo == | ||
| + | |||
| + | *[http://www.definicionabc.com/general/rectas-paralelas.php Definición ABC] <br> | ||
| + | |||
| + | == Fuentes == | ||
| − | + | *[http://www.escolar.com/avanzado/geometria008.htm Contenidos de Escolar. com ]<br> | |
| − | * | + | *[http://www.vitutor.com/geo/rec/e_9.html Vitutor ]<br> |
| − | + | *[http://www.escueladigital.com.uy/geometria/1_lineas.htm Escuela Digital ]<br> | |
| − | + | *[http://concepbas.blogspot.com/ Conceptos Básicos ]<br> | |
| − | * | ||
| − | * | ||
| − | * | ||
[[Category:Fundamentos_de_la_Geometría]] | [[Category:Fundamentos_de_la_Geometría]] | ||
Revisión del 15:21 31 mar 2011
| ||||||
Recta Oblícua es cuando se cruzan en forma inclinada entre ellas, y por lo tanto dividen el plano en cuatro sectores de los cuales dos son iguales, pero distintos de los otros dos que a su vez son iguales entre sí. Es decir que forma con otra línea un ángulo que no es recto
Sumario
Recta
Recta La línea es aquella que representa un conjunto de puntos. Una idea de recta nos la da un hilo extendido, o bien, el borde de una regla. Toda recta es limitada, las flechas indican que la recta se prolonga indefinidamente en ambos sentidos. Para referirnos a una recta (notación) se pueden seleccionar dos de sus puntos a los que se asocian letras mayúsculas.
Definiciones de rectas oblicuas
- Toda recta que corta a una recta formando un ángulo que no es recto, se dice que es oblicua a la recta.
- Que no es perpendicular ni paralelo a un plano, a una recta, o a una dirección determinada.
- Si dos rectas tienen un punto de intersección, y forman ángulos no todos iguales, las rectas se llaman oblicuas.
Clases de rectas en un plano
Dos rectas o más pueden encontrarse entre sí en distintas posiciones posibles:
- Dos rectas ubicadas en el mismo plano se denominan Rectas Paralelas cuando todos los puntos de ambas se encuentran a la misma distancia.
- Dos rectas ubicadas en el mismo plano se denominan divergentes cuando los puntos de ambas van aumentando su distancia.
- Dos rectas ubicadas en el mismo plano se denominan convergentes cuando los puntos de ambas van dismuyendo su distancia; y eventualmente ambas rectas se cruzan en un punto.
Es fácil advertir que en los dos últimos casos, en realidad se está haciendo referencia a semirrectas; por cuanto las divergentes resultan convergentes si se invierte el sentido de la comparación de sus distancias, y las convergentes, luego de cruzarse, se tornan divergentes.
Clases de rectas convergentes
Las rectas convergentes, pueden ser:
- Rectas Perpendiculares: cuando dividen el plano en cuatro partes iguales; es decir, cuando al cruzarse ninguna resulta estar inclinada respecto de la otra.
- Rectas Oblicuas :cuando se cruzan en forma inclinada entre ellas, y por lo tanto dividen el plano en cuatro sectores de los cuales dos son iguales, pero distintos de los otros dos que a su vez son iguales entre sí.
Podemos nombrar tres posiciones si hablamos de la relación que se haya entre dos líneas rectas; éstas pueden ser paralelas, perpendiculares, u oblicuas, entre sí. Dos líneas paralelas siempre permanecen equidistantes, lo que significa que se hayan entre sí a la misma distancia en todos sus puntos; además, no se cruzan nunca. Una línea recta es perpendicular a otra cuando la corta formando ángulos de 90º.
Propiedades de rectas oblicuas
Rectas oblicuas.
Si desde un punto exterior a una recta se traza la perpendicular y varias oblicuas:
- La perpendicular es menor que cualquier oblicua.
- Las oblicuas que tiene la misma distancia del pie de la perpendicular son igual.
- Si dos oblicuas tiene diferente medida del pie de la perpendicular, es mayor la que más se aparta.
Las líneas rectas oblicuas se originan en puntos diferentes, pero luego se cruzan, dando lugar a ángulos agudos y obtusos (nunca rectos).