Diferencia entre revisiones de «Usuario:Humberto0601ad jc/Felo»
| Línea 34: | Línea 34: | ||
3.2. S ← S ∪ {w} //Se agrega w al conjunto S, pues ya se //tiene el camino mínimo hacia w | 3.2. S ← S ∪ {w} //Se agrega w al conjunto S, pues ya se //tiene el camino mínimo hacia w | ||
3.3. Para cada v∈(V-S) hacer | 3.3. Para cada v∈(V-S) hacer | ||
| − | 3.3.1. D[v] ← min(D[v],D[w]+C[w,v]) //Se escoge, entre | + | 3.3.1. D[v] ← min(D[v],D[w]+C[w,v]) //Se escoge, entre //el camino mínimo hacia v que se tiene //hasta el momento, y el camino hacia v //pasando por w mediante su camino mínimo, //el de menor costo. |
| − | //el camino mínimo hacia v que se tiene //hasta el momento, y el camino hacia v //pasando por w mediante su camino mínimo, //el de menor costo. | ||
3.3.2. Si min(D[v],D[w]+C[w,v]) = D[w]+C[w,v] entonces P[v] ← w //Si se escoge ir por w entonces //el predecesor de v por el momento es w | 3.3.2. Si min(D[v],D[w]+C[w,v]) = D[w]+C[w,v] entonces P[v] ← w //Si se escoge ir por w entonces //el predecesor de v por el momento es w | ||
'''Paso 4. Fin ''' | '''Paso 4. Fin ''' | ||
| − | == | + | == Ejecución de algoritmo == |
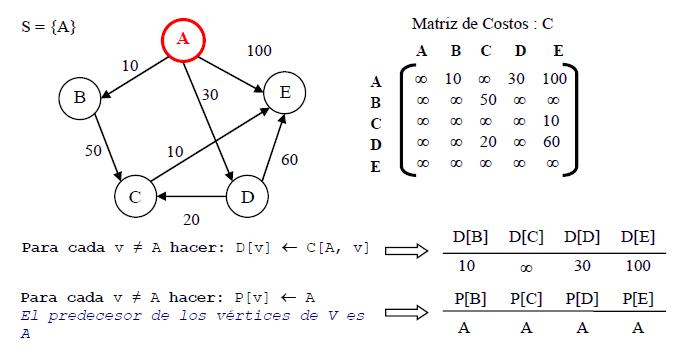
| + | ''' Paso 1:''' Inicialización | ||
| + | [[Image:Algo02.JPG]] | ||
| + | |||
| + | ''' Paso 2: ''' Elegir un vértice w ∈ V - {A} tal que D[w] sea mínimo, y agregar w al conjunto solución S | ||
| + | [[Image:Algo03.JPG]] | ||
| + | |||
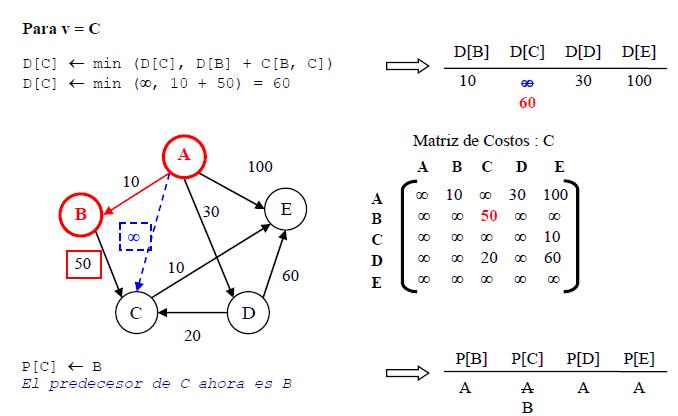
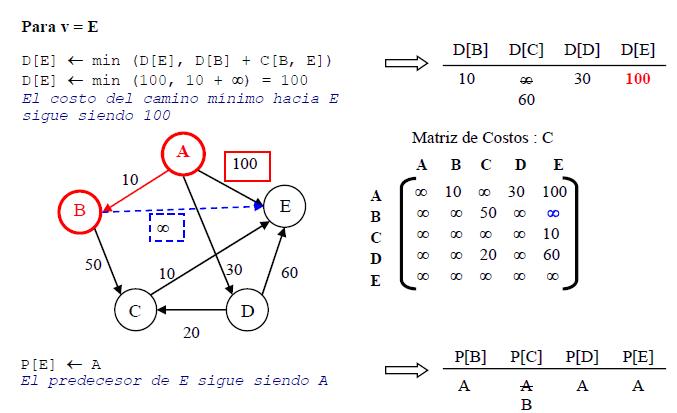
| + | ''' Paso 3: ''' cada v ∈ {C, D, E} hacer D[v] ← min( D[v], D[w]+C[w, v] ) | ||
| + | [[Image:Algo04.JPG]] | ||
| + | |||
| + | [[Image:Algo05.JPG]] | ||
| + | |||
| + | [[Image:Algo06.JPG]] | ||
== rt == | == rt == | ||
Revisión del 15:18 1 abr 2011
| ||||||
En múltiples aplicaciones donde se aplican los grafos, es necesario conocer el camino de menor costo entre dos vértices dados:
- Distribución de productos a una red de establecimientos comerciales.
- Distribución de correos postales.
- Sea G = (V, A) un grafo dirigido ponderado.
El problema del camino más corto de un vértice a otro consiste en determinar el camino de menor costo, desde un vértice u a otro vértice v. El costo de un camino es la suma de los costos (pesos) de los arcos que lo conforman.
Características del algoritmo
- Es un algoritmo greddy.
- Trabaja por etapas, y toma en cada etapa la mejor solución sin considerar consecuencias futuras.
- El óptimo encontrado en una etapa puede modificarse posteriormente si surge una solución mejor.
Pasos del algoritmo
Algoritmo 24.1: Algoritmo de Dijkstra. Inicialización.
- Sea V un conjunto de vértices de un grafo.
- Sea C una matriz de costos de las aristas del grafo, donde en C[u,v] se almacena el costo de la arista entre u y v.
- Sea S un conjunto que contendrá los vértices para los cuales ya se tiene determinado el camino mínimo.
- Sea D un arreglo unidimensional tal que D[v] es el costo del camino mínimo del vértice origen al vértice v.
- Sea P un arreglo unidimensional tal que P[v] es el vértice predecesor de v en el camino mínimo que se tiene construido.
- Sea vinicial el vértice origen. Recordar que el Algoritmo Dijkstra determina los caminos mínimos que existen partiendo de un vértice origen al resto de los vértices.
Paso 1. S ← {vinicial} //Inicialmente S contendrá el vértice //origen
Paso 2. Para cada v∈V, v ≠ vinicial, hacer
2.1. D[v] ← C[vinicial, v] //Inicialmente el costo del //camino mínimo de vinicial a v es lo contenido en //la matriz de costos
2.2. P[v] ← vinicial //Inicialmente, el //predecesor de v en el camino mínimo construido //hasta el momento es vinicial
Paso 3. Mientras (V – S ≠ ∅) hacer //Mientras existan vértices para //los cuales no se ha determinado el //camino mínimo
3.1. Elegir un vértice w∈(V-S) tal que D[w] sea el mínimo.
3.2. S ← S ∪ {w} //Se agrega w al conjunto S, pues ya se //tiene el camino mínimo hacia w
3.3. Para cada v∈(V-S) hacer
3.3.1. D[v] ← min(D[v],D[w]+C[w,v]) //Se escoge, entre //el camino mínimo hacia v que se tiene //hasta el momento, y el camino hacia v //pasando por w mediante su camino mínimo, //el de menor costo.
3.3.2. Si min(D[v],D[w]+C[w,v]) = D[w]+C[w,v] entonces P[v] ← w //Si se escoge ir por w entonces //el predecesor de v por el momento es w
Paso 4. Fin
Ejecución de algoritmo
Paso 2: Elegir un vértice w ∈ V - {A} tal que D[w] sea mínimo, y agregar w al conjunto solución S

Paso 3: cada v ∈ {C, D, E} hacer D[v] ← min( D[v], D[w]+C[w, v] )