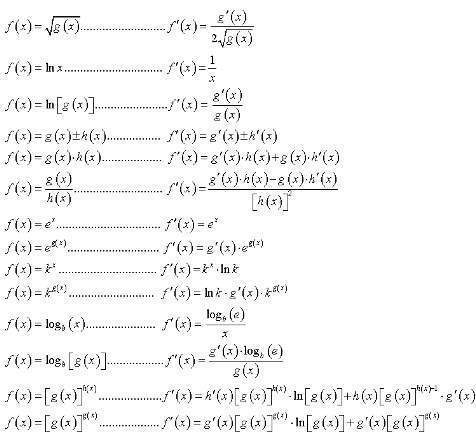Diferencia entre revisiones de «Reglas de derivación»
| Línea 1: | Línea 1: | ||
{{Desarrollo}} {{Objeto|nombre= Reglas de derivación|imagen= Aprenda_a_derivar.jpg |descripcion= Regla de derivación para calcular la derivada de potencias de exponente natural}} '''Reglas de derivación.''' Son reglas que permiten efectuar el cálculo de derivadas de funciones. | {{Desarrollo}} {{Objeto|nombre= Reglas de derivación|imagen= Aprenda_a_derivar.jpg |descripcion= Regla de derivación para calcular la derivada de potencias de exponente natural}} '''Reglas de derivación.''' Son reglas que permiten efectuar el cálculo de derivadas de funciones. | ||
| + | |||
| + | == Otras Derivadas == | ||
| + | |||
| + | [[Image:Otras derivadas.jpg]] | ||
| + | |||
| + | == Ejemplos == | ||
| + | |||
| + | a) f(x)= 5 f ´(x)= 0 | ||
| + | |||
| + | b) f(x)= X f ´(x)= 1<br> | ||
| + | |||
| + | |||
| + | |||
| + | <br> | ||
== Reglas de derivación == | == Reglas de derivación == | ||
| Línea 26: | Línea 40: | ||
[[Image:Regla de la cadena.jpg]] | [[Image:Regla de la cadena.jpg]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Tabla de derivadas == | == Tabla de derivadas == | ||
Revisión del 15:49 3 may 2011
| ||||
Reglas de derivación. Son reglas que permiten efectuar el cálculo de derivadas de funciones.
Sumario
Otras Derivadas
Ejemplos
a) f(x)= 5 f ´(x)= 0
b) f(x)= X f ´(x)= 1
Reglas de derivación
Si f (x) y g (x) son derivables en el punto Xo , se cumple:
La derivada de una constante por una función es la constante por la derivada de la función
La derivada de la suma de dos funciones es la suma de las derivadas de cada una de las funciones.
La derivada de un producto de dos funciones es igual a la suma del producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función sin derivar
La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado
Reglas de la cadena
La regla de la cadena es una fórmula para la derivada de la composición de dos funciones.
Tabla de derivadas
Bibliografía
- Cálculo. Roland Larson y otros.
- Cálculo Diferencial e Integral, Willian Granville y otros