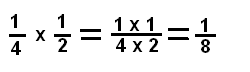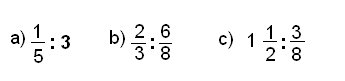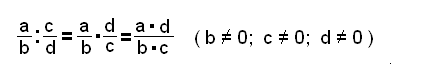Diferencia entre revisiones de «Multiplicación y división de fracciones comunes»
| Línea 1: | Línea 1: | ||
| + | La '''multiplicación y división de fracciones comunes'''. Muy utilizadas en la vida práctica ante situaciones dadas generalmente para compartir y / o repartir algo. | ||
| + | |||
| + | |||
{{Definición | {{Definición | ||
|nombre=Multiplicación y división de fracciones comunes. | |nombre=Multiplicación y división de fracciones comunes. | ||
| Línea 4: | Línea 7: | ||
|= | |= | ||
|concepto=El concepto matemático de fracción, corresponde a la idea intuitiva de dividir una totalidad en partes iguales. Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria. | |concepto=El concepto matemático de fracción, corresponde a la idea intuitiva de dividir una totalidad en partes iguales. Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria. | ||
| − | La fracción está formada por dos términos: el numerador y el denominador | + | La fracción está formada por dos términos: el numerador y el denominador: a / b (a sobre b). |
| − | |||
'''a''' NUMERADOR: indica las partes que se toman. | '''a''' NUMERADOR: indica las partes que se toman. | ||
'''b''' DENOMINADOR: indica las partes iguales en que se divide la unidad. | '''b''' DENOMINADOR: indica las partes iguales en que se divide la unidad. | ||
| − | |||
}} | }} | ||
| − | == | + | == Reseña histórica == |
La teoría y el cálculo de las fracciones como la utilizamos en la actualidad, se le atribuye al matemático hindú [[Brahmagupta]] (600 años a.n.e.). Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con [[fracciones]] de una forma más simple. | La teoría y el cálculo de las fracciones como la utilizamos en la actualidad, se le atribuye al matemático hindú [[Brahmagupta]] (600 años a.n.e.). Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con [[fracciones]] de una forma más simple. | ||
| − | == Multiplicación | + | == Multiplicación de fracciones comunes == |
Al igual que los [[números naturales]], las fracciones se pueden multiplicar. | Al igual que los [[números naturales]], las fracciones se pueden multiplicar. | ||
Por ejemplo: | Por ejemplo: | ||
| Línea 31: | Línea 32: | ||
En los ejemplos anteriores has visto diferentes representaciones para la multiplicación de fracciones, en todos los casos el producto se calcula de la misma forma: | En los ejemplos anteriores has visto diferentes representaciones para la multiplicación de fracciones, en todos los casos el producto se calcula de la misma forma: | ||
| − | + | Observa que: | |
[[Archivo:imagen 4.PNG]] | [[Archivo:imagen 4.PNG]] | ||
| Línea 41: | Línea 42: | ||
En todos los casos se han multiplicado las fracciones multiplicando numerador por numerador y denominador por denominador. | En todos los casos se han multiplicado las fracciones multiplicando numerador por numerador y denominador por denominador. | ||
| − | + | Veamos otros ejemplos: | |
Halla el producto de las siguientes fracciones: | Halla el producto de las siguientes fracciones: | ||
| Línea 55: | Línea 56: | ||
[[Archivo:imagen 10.PNG]] | [[Archivo:imagen 10.PNG]] | ||
| − | + | En resumen: | |
| − | |||
| − | + | La multiplicación de fracciones se realiza multiplicando los | |
| + | numeradores y multiplicando los denominadores entre sí. Es | ||
| + | conveniente, antes de calcular el producto simplificar tanto como | ||
| + | sea posible de lo contrario deberás hacerlo en la fracción | ||
| + | resultante. | ||
| + | |||
| + | De forma general: | ||
[[Archivo:imagen 11.PNG]] | [[Archivo:imagen 11.PNG]] | ||
| Línea 71: | Línea 77: | ||
Dada una fracción, para formar su recíproco, basta invertir sus términos. | Dada una fracción, para formar su recíproco, basta invertir sus términos. | ||
| − | |||
== Ejemplos == | == Ejemplos == | ||
| Línea 104: | Línea 109: | ||
10 El recíproco de _5_ es _10_ = 2. | 10 El recíproco de _5_ es _10_ = 2. | ||
10 5 | 10 5 | ||
| − | |||
| Línea 113: | Línea 117: | ||
[[Archivo:imagen 12.PNG]] | [[Archivo:imagen 12.PNG]] | ||
| − | |||
La mitad de un huerto escolar la divides en cuatro partes iguales para sembrar lechugas en una de ellas, ¿qué parte del terreno se dedicará a ese tipo de hortalizas? | La mitad de un huerto escolar la divides en cuatro partes iguales para sembrar lechugas en una de ellas, ¿qué parte del terreno se dedicará a ese tipo de hortalizas? | ||
[[Archivo:imagen 13.PNG]] | [[Archivo:imagen 13.PNG]] | ||
| − | |||
Para hallar qué parte es un conjunto de otro, debes dividir. Luego también podemos darle este significado a la división de fracciones , por ejemplo: | Para hallar qué parte es un conjunto de otro, debes dividir. Luego también podemos darle este significado a la división de fracciones , por ejemplo: | ||
| Línea 130: | Línea 132: | ||
En todos los casos se han dividido las fracciones reduciéndolas a una multiplicación donde el segundo factor es el recíproco del divisor. | En todos los casos se han dividido las fracciones reduciéndolas a una multiplicación donde el segundo factor es el recíproco del divisor. | ||
| − | |||
== Ejemplos == | == Ejemplos == | ||
| Línea 155: | Línea 156: | ||
En general: | En general: | ||
[[Archivo:imagen 20.PNG]] | [[Archivo:imagen 20.PNG]] | ||
| − | |||
Revisión del 09:28 7 jun 2011
La multiplicación y división de fracciones comunes. Muy utilizadas en la vida práctica ante situaciones dadas generalmente para compartir y / o repartir algo.
Sumario
Reseña histórica
La teoría y el cálculo de las fracciones como la utilizamos en la actualidad, se le atribuye al matemático hindú Brahmagupta (600 años a.n.e.). Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con fracciones de una forma más simple.
Multiplicación de fracciones comunes
Al igual que los números naturales, las fracciones se pueden multiplicar. Por ejemplo: Si quieres saber el tiempo que inviertes en practicar la ortografía dedicando ¼ (un cuarto) de hora 3 veces a la semana, ¿cómo lo planteas?.
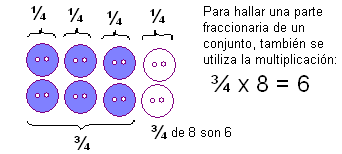
¿Necesitas conocer cuántos botones representan ¾ (tres cuartas) partes de un conjunto de 8 botones?
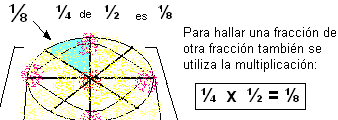
¿Quieres saber qué parte del pastel se comió tu hermanita si le sirvieron ¼ (un cuarto) de la mitad del pastel?
En los ejemplos anteriores has visto diferentes representaciones para la multiplicación de fracciones, en todos los casos el producto se calcula de la misma forma:
Observa que:
En todos los casos se han multiplicado las fracciones multiplicando numerador por numerador y denominador por denominador.
Veamos otros ejemplos:
Halla el producto de las siguientes fracciones:
¿Cómo los resolvemos?:
En resumen:
La multiplicación de fracciones se realiza multiplicando los numeradores y multiplicando los denominadores entre sí. Es conveniente, antes de calcular el producto simplificar tanto como sea posible de lo contrario deberás hacerlo en la fracción resultante.
De forma general:
Recíproco de una fracción
Antes de comenzar el estudio de la división de fracciones, es necesario que aprendas qué es el recíproco de una fracción, lo necesitarás en el procedimiento a seguir para dividir.
Definición 1
El recíproco de una fracción es la fracción
donde
.
Dada una fracción, para formar su recíproco, basta invertir sus términos.
Ejemplos
Halla el recíproco de:
a) _1_
3
b) 2
c) _7_
4
d) 0,5
Respuestas:
a) _1_ igual a _3_ Invirtiendo el numerador y el denominador.
3 1 El recíproco de _1_ es 3.
3
b) 2 igual a ½ El recíproco de 2 es ½ (un medio).
c) _7_ igual a _4_ El recíproco de _7_ es _4_.
4 7 4 7
d) 0,5 igual a _5_ Se escribe la expresión decimal como fracción.
10 El recíproco de _5_ es _10_ = 2.
10 5
División de fracciones comunes
En los números naturales la división significa repartir en partes iguales, con las fracciones también se le puede dar esa interpretación y resolver situaciones prácticas, por ejemplo: Tienes 5 naranjas y las picas exactamente a la mitad ¿cuántas partes tienes ahora?
La mitad de un huerto escolar la divides en cuatro partes iguales para sembrar lechugas en una de ellas, ¿qué parte del terreno se dedicará a ese tipo de hortalizas?
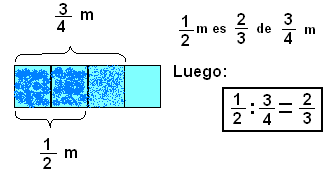
Para hallar qué parte es un conjunto de otro, debes dividir. Luego también podemos darle este significado a la división de fracciones , por ejemplo: ¿Qué parte es ½ m de tela de ¾ m?
Independientemente de las diferentes interpretaciones que puede tener la división, para calcular existe un único procedimiento como podemos observar a continuación:
En todos los casos se han dividido las fracciones reduciéndolas a una multiplicación donde el segundo factor es el recíproco del divisor.
Ejemplos
Halla el cociente:
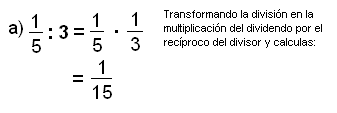
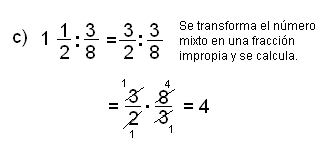
Para resolverlos:
En resumen
La división de fracciones se realiza transformándola en una multiplicación en la cual el primer factor es el dividendo y el segundo es el recíproco del divisor. Luego se procede como en la multiplicación.
En general:
Fuentes
- Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, 1990.
- `Profesorenlinea.cl