Diferencia entre revisiones de «Ángulos en la circunferencia»
| Línea 3: | Línea 3: | ||
|imagen=Presentac.PNG | |imagen=Presentac.PNG | ||
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto= Se le llama [[circunferencia]] al conjunto de puntos situados a la misma distancia de otro punto llamado centro. |
| + | |||
Un [[ángulo]] es la parte del plano limitada por dos semirrectas que parten del mismo punto: el vértice. | Un [[ángulo]] es la parte del plano limitada por dos semirrectas que parten del mismo punto: el vértice. | ||
}}<div align=justify> | }}<div align=justify> | ||
| − | '''Ángulos en la circunferencia.''' En la enseñanza de la [[ | + | '''Ángulos en la circunferencia.''' En la enseñanza de la [[matemática]] se utiliza los conceptos y teoremas fundamentales de forma estructurada, lo que para la [[geometría]] tiene sus particularidades. |
| + | |||
| + | Existen las definiciones de los conceptos de [[ángulo]] central, inscrito y semi-inscrito que se podeden utilizar para obtener algunos resultados geométricos importantes. | ||
== Aplicaciones == | == Aplicaciones == | ||
| − | En la enseñanza de la | + | En la enseñanza de la geometría se comprenden de forma fragmentada los conceptos y teoremas, y su utilización en la resolución de problemas es muy limitada. |
| − | La | + | |
| − | El tratamiento de estos conceptos en la solución de problemas de este tipo, posibilita la formación de una visión global inicial de las habilidades matemáticas para calcular longitudes de segmentos, arcos y amplitudes de | + | La Geometría está encaminada a prepararse para resolver problemas geométricos de construcción, de cálculo y de demostración a partir de las relaciones de [[igualdad de triángulos]], en la [[circunferencia]] y la semejanza. |
| + | |||
| + | El tratamiento de estos conceptos en la solución de problemas de este tipo, posibilita la formación de una visión global inicial de las habilidades matemáticas para calcular longitudes de segmentos, arcos y amplitudes de ángulos en situaciones dadas. | ||
| + | |||
== Ángulo central == | == Ángulo central == | ||
[[Archivo:Ángulo_central.PNG]] | [[Archivo:Ángulo_central.PNG]] | ||
Revisión del 15:07 27 jun 2011
| ||||||
Ángulos en la circunferencia. En la enseñanza de la matemática se utiliza los conceptos y teoremas fundamentales de forma estructurada, lo que para la geometría tiene sus particularidades.
Existen las definiciones de los conceptos de ángulo central, inscrito y semi-inscrito que se podeden utilizar para obtener algunos resultados geométricos importantes.
Sumario
Aplicaciones
En la enseñanza de la geometría se comprenden de forma fragmentada los conceptos y teoremas, y su utilización en la resolución de problemas es muy limitada.
La Geometría está encaminada a prepararse para resolver problemas geométricos de construcción, de cálculo y de demostración a partir de las relaciones de igualdad de triángulos, en la circunferencia y la semejanza.
El tratamiento de estos conceptos en la solución de problemas de este tipo, posibilita la formación de una visión global inicial de las habilidades matemáticas para calcular longitudes de segmentos, arcos y amplitudes de ángulos en situaciones dadas.
Ángulo central
Los lados del ángulo central son radios de la circunferencia por lo que OA = OB. La amplitud de un arco es igual a la amplitud de su ángulo central correspondiente.
Relación entre ángulos centrales
Observemos que, en una misma circunferencia, o en circunferencias iguales, a ángulos centrales iguales corresponden arcos iguales.
Véase también que, en una misma circunferencia, o en circunferencias iguales, a ángulos centrales iguales corresponden arcos ycuerdas iguales y, a mayor cuerda corresponde mayor arco y viceversa.
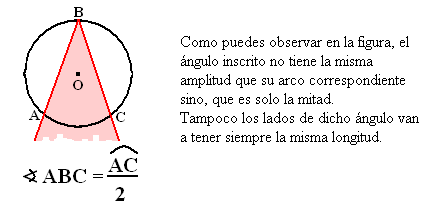
Ángulo inscrito en una circunferencia
Un ángulo cuyo vértice pertenece a una circunferencia y sus lados la intersecan además en otros dos puntos se denomina ángulo inscrito en la circunferencia.
La demostración de lo planteado en la figura puede verse en:
[*http://apuntes-dematematicas.blogspot.com/2009/03/circunferencias.html] Definición 5.1.2
Relación entre ángulos inscritos
Ángulo semi-inscrito
Véase también
Fuente
- Libro de texto de Matemática 8vo grado. Editorial Pueblo y Educación, 1990.