Proporcionalidad compuesta
En los problemas de proporcionalidad compuesta intervienen tres variables, siendo una de ellas la variable incógnita. La relación entre las variables con la variable incógnita puede ser una proporcionalidad simple directa o inversa. Se resuelven aplicando una regla de tres compuesta.
Ejemplo
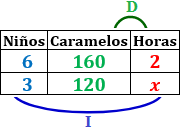
Problema: si 6 niños comen 160 caramelos en 2 horas, ¿cuántas horas tardan 3 niños en comer 120 caramelos?
Resolución
Variables: Las variables del problema son: (número de) niños, (número de) caramelos y (número de) horas. La variable incógnita es horas.
Relación entre las variables (con la variable incógnita):
- Niños-horas: cuantos más niños hay, menos horas tardan en comer los caramelos. Es una proporcionalidad inversa.
- Caramelos-horas: cuantos más caramelos hay, más horas tardan en comerlos. Es una proporcionalidad directa.
Tabla con los datos: escribimos una tabla con los datos, dejando la variable incógnita en la tercera columna e indicamos con flechas si se trata de una proporcionalidad directa (D) o inversa (I).
Regla de tres compuesta: Escribimos las dos columnas de la izquierda como dos fracciones que se multiplican e igualamos con la columna derecha:
Importante:
- Si es una proporcionalidad directa, escribimos la primera fila dividido entre la segunda.
- Si es una proporcionalidad inversa, escribimos la segunda fila dividido entre la primera.
Calculamos la incógnita despejando la x:
Por tanto, 3 niños tardan 3 horas en comer 120 caramelos.