Función lineal
| ||||||
Función lineal: La función que a cada x€R le hace corresponder un número real f(x) = mx + n. Donde m y n son números reales dados, se denomina función lineal.
Sumario
Características generales
Una función lineal según la primera definición dada anteriormente representa una aplicación lineal si y sólo si n = 0. Así, algunos autores llaman función lineal a aquella de la forma mientras que llaman función afín a la que tiene la forma
, cuando n es distinto de cero. La grafica de la función lineal es una recta.
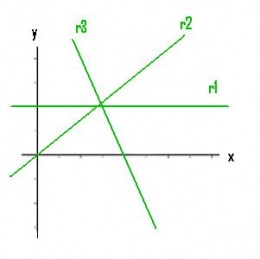
Los valores de m y n son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y n es el punto de corte de la recta con el eje y. Cuando cambiamos m modificamos la inclinación de la recta y cuando cambiamos n desplazamos la línea arriba o abajo.
Pendiente
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m < 0, la recta se inclina hacia arriba, la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.
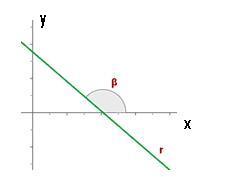
Si m > 0, la recta se inclina hacia abajo, la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.
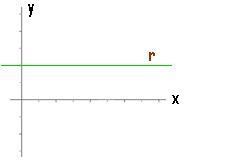
Si m = 0, la recta es paralela al eje x.
Cero de la función
El dominio de la función lineal es el conjunto de los números reales.
El elemento del dominio de la función lineal f(x) = mx + n (m ≠0) cuya imagen es cero, se denomina cero de esta función.
Calculo de la pendiente de la recta
La pendiente m de la recta que pasa por los punto P1(x1; y1) y P2(x2; y2) se calcula por la fórmula
Véase también
Fuente
- Baño Muñoz Felix. Colectivo de autores. Matemática 8vo grado.Editorial Pueblo y Educación. 1991.