Pirámide
| ||||||
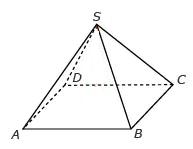
Pirámide (Figura). Es un poliedro limitado por una base, que es un polígono cualquiera, y varias caras laterales, que son triángulos con un vértice común llamado vértice de la pirámide.
Sumario
Área
Como cualquier poliedro, la pirámide posee área. En dependencia de lo que se quiere calcular podemos calcular su área de la base, área lateral, o el área total.
Área de la base
Como la base de la pirámide, puede ser cualquier polígono, entonces llamamos área de la base(Ab) de la pirámide, al área del polígono que conforma su base, independientemente de su clasificación, por ejemplo, la base de la pirámide puede ser un triángulo, un cuadrilátero, etc.
Área lateral
Las caras laterales de la pirámide son triángulos, y habrá tantas caras laterales como lados tenga el polígono de la base. Entonces el área lateral de la pirámide(AL) se calcula como la suma de todas las áreas de los triángulos que conforman las caras laterales. AL =A1 + A2 + A3 + ……
Área total
El área total de la pirámide (AT) se calcula como la suma de su área de la base(Ab) y el área lateral (AL), es decir, con la fórmula: AT = Ab + AL
Volumen
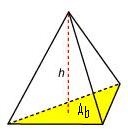
Supongamos que tenemos una pirámide de altura (h) y que la superficie (área) de su base tiene un valor Ab.El volumen (V)de la pirámide vendría dado por la fórmula:
Donde V, Ab, y h deben ir expresadas en unidades de medida que se correspondan; por ejemplo, si h se expresa en cm, Ab irá en cm2 y V en cm3.
Nota: el volumen de una pirámide es una tercera parte del volumen de un prisma recto que tenga la misma base y la misma altura.