Funciones continuas
| ||||
Funciones continuas. Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.
Sumario
Definición
Una función f es continua en un número a si y sólo si se satisfacen las tres condiciones siguiente:
i) f (a) existe;
ii) Archivo:Limite.jpg existe;
iii) Archivo:Continuidad.jpg
Si por lo menos una de estas tres condiciones no se cumple en a, entonces se dice que la función f es discontinua en a.
Ejemplo
Estudiar la continuidad de en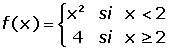
x =2
i) f(2)= 4 existe
ii)Archivo:Continuidad2.jpg
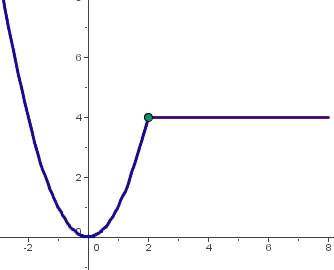Cumple las tres condiciones por lo que la función es continua.
Continuidad lateral
Continuidad por la izquierda
Una función f(x) es continua por la izquierda en el punto x = a si:
Archivo:Continuidad5.jpg
Continuidad por la derecha
Una función f(x) es continua por la derecha en el punto x = a si:
Una función f es continua en un punto si es continua por la izquierda y es continua por la derecha:
Función discontinua
Para que una función sea discontinua f(x) sea discontinua en un punto deberá darse una, al menos, de estas condiciones:
Dependiendo de qué condición se verifique, los puntos en los que una función no es continua se clasifican en puntos de discontinuidad evitable y en puntos de discontinuidad no evitable (o inevitable).
Discontinua Evitable.
Es evitable si existen f(a) y es un número real, pero no coinciden. Se evita la discontinuidad haciendo
Ejemplo: La función definida por es discontinua en 2, pues dicha función no está definida en el 2.
Cuando una función f presenta las características anteriores, es decir, no está definida en un número a pero existe, se dice que f presenta una discontinuidad evitable, porque si f es redefinida en a de manera que la nueva función es continua en a.
La discontinuidad de la función es evitable, porque si se redefine en 2, se obtiene la siguiente función:
La función F es continua en todos los puntos
Discontinua no evitable
Se divide en discontinuidad de primera especie, existen los límites laterales en el punto pero no coinciden
Salto finito, los dos límites laterales son un número real, el salto es la diferencia entre los límites laterales.
Salto infinito, uno de los límites laterales es infinito.
Discontinuidad asintótica, si los dos limites laterales de la función en el punto x0 son infinitos:
De segunda especie, si la función no existe en uno de los lados del punto, o no existen alguno, o ambos, de los limites laterales de la función en ese punto, se dice que la función presenta una discontinuidad de segunda especie en ese punto..
Ejemplo 1:
Estudiar la continuidad de la función
Rta) f(0) no existe, el valor x=0 no está incluido ni por la izquierda ni por la derecha
Calculamos los límites laterales en x=0
no existe límite
Existe una discontinuidad de salto finito de 6 unidades
Ejemplo 2: Estudiar la continuidad de la función
f(x) =
Rta)
No existe y no existe . En x=-2 y x=2 la función presenta discontinuidades no evitables de 2 segunda especie.
Fuente
Continuidad de una finción
Funciones continuas
Clasificación de las discontinuidades
