Número complejo
Números Complejos. Conjunto numérico surgido para resolver soluciones de raíces negativas.
Sumario
Definición.
Los números reales, a pesar de su utilidad y universalidad presentan la gran deficiencia de que: no toda función polinómica tiene una raíz.
Un singular y notable ejemplo es la ecuación de segundo grado x2 + 1=0, de donde se obtiene que x2 = -1. Pero según las reglas del álgebra ningún número positivo o negativo elevado al cuadrado puede dar -1, es decir no existe ningún número x que satisfaga la ecuación del anterior ejemplo.
La insuficiencia antes planteada ha obligado a los matemáticos a inventar un número i, con la propiedad de que i2 + 1 =0, la admisión de este número dentro de la gran familia de los números ha simplificado considerablemente los cálculos algebraicos.
Representaciones de números complejos.
Los números complejos tienen varias formas de representación. A saber:
- Representación puntual.
- Representación algebraica.
- Representación trigonométrica.
- Representación exponencial.
Representación puntual.
Se representa el número z como un punto del plano en coordenadas cartesianas (x, y), donde x es la parte real y y el componente imaginario.
Nótese que otras formas de representacion del punto en el plano, como las coordenadas polares no se incluyen en esta forma de representación puntal del número complejo.
Representación algebraica.
El número complejo z se representa por una expresión algebraica x+yi, donde x es la parte real y y el componente imaginario.
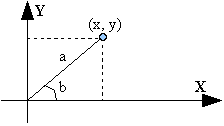
Representación trigonométrica.
La representación trigonométrica de un número complejo se basa en la representación de un punto por coordenadas polares (a, b) donde a es la longitud del radio vector hasta el punto en cuestión y b el ángulo respecto a eje de las X.
Luego puede representarse al número complejo z = x + yi como z = acos(b)+aisen(b) donde las representaciones se relacionan de la siguiente manera:
Aritmética de los números complejos.
Los números complejos soportan las operaciones aritméticas elementales:
- Adición.
- Sustracción.
- Multiplicación.
- División.
Adición.
Sean los números complejos z1 y z2, definidos en notación algebraica como:
z1=x1</sub+y1i z2=x2</sub+y2i
la suma de ambos vendrá dada por el resultado:
z3=z1+z2=(x1+x2)+i(y1+y2).�
Sustracción: Sí z1 =x1+y1i, z2=x2 + y2i, entonces z1 – z2 = (x1 – x2) – i (y1 – y2)
Multiplicación: Sí z1 =x1 + iy1, z2 =x2 + iy2, entonces z1·z2 = (x1x2 –y1y2) + i (x1y2 – x2y1), los números complejos se multiplican como binomios y en este caso i2 se sustituye por -1
La multiplicación de los números complejos se subordina a las leyes conmutativa, asociativa y distributiva (respecto a la adición)
z1·z2 = z2·z1; (z1·z2) ·z3 = z3·z2) ·z1= z1·z2·z3; z1· (z2+ z3) = (z1· z2)+ z3
División: Para determinar el cociente de dos números complejos representados en la forma algebraica es necesario multiplicar el dividendo y el divisor por el número conjugado con el divisor.
El conjugado de un número complejo z = x + iy se define como z* = x – iy.
Relación de los complejos con otros conjuntos numéricos.
Fuentes.
- Michael Spivak. Cálculo infinitesimal.
- P. E. Danko, A. G. Popov y T. YA. Kozhenikova. Matemática superiores en ejercicios y problemas.