Inecuaciones fraccionarias

Inecuaciones fraccionarias 260px Concepto: Son inecua­ciones que tienen una fracción algebraica formando parte de la misma.

Inecuaciones fraccionarias. Inecuaciones en las que cada término es una fracción racional, o cociente de polinomios.

Definición

Para comprender el contenido al que se hace referencia, es necesario conocer la siguiente definición:

Inecuaciones

Desigualdades algebraicas en la que sus dos miembros se relacionan por los signos: mayor, menor, mayor o igual o menor o igual. La solución de una inecuación es el conjunto de valores de la variable que la verifica, donde la solución se expresa mediante una representación gráfica y/o mediante un intervalo.

Para dar solución a una inecuación hay que tener en cuenta que:

• Una inecuación se verifica solo para algunos valores de las va­riables.
• Los valores numéricos para los cuales se verifica la desigualdad son las soluciones de la misma.
• Resolver una inecuación consiste en hallar los valores numéricos para los cuales la desigualdad es verdadera.

Regla general para resolver una inecuación

Se sigue el mismo procedimiento que para resolver una ecuación (quitar denominadores, términos, agrupar, etc), pero hay que tener en cuenta, al multiplicar o dividir por cantidades negativas que tenemos que cambiar el sentido de la desigualdad para que el resultado no varíe.

Método de resolución de las inecuaciones fraccionarias

Las inecuaciones fraccionarias o racionales tienen incognitas tanto en el numerador como en el denominador y se resuelven de un modo similar a las de segundo grado, pero hay que tener presente que el denominador no puede ser cero.

Para encontrar la solución hay que descomponer factorialmente los polinomios nume­rador y denominador, aplican­do Ruffini, complitud de cuadrados, etc. … el método que consideres más apropiado o que mejor te resulte. Una vez descom­puestos nunca simplificar ya que podríamos perder soluciones. Posterior­mente se procede como con las inecuaciones de grado mayor que uno, ya que se trata en el fondo de averiguar el signo final que va a tener un cociente de productos de binomios.

Ejemplos de inecuaciones fraccionarias

• Se calculan las raíces del numerador y del denominador.

x-2=0
x=2

x-4=0
x=4

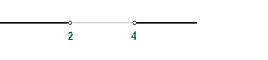
• Se representan estos valores en la recta real, teniendo en cuenta que las raíces del denominador, independientemente del signo de la desigualdad, tienen que ser abiertas.
• Se toma un punto de cada intervalo y se evalúa el signo en cada intervalo.

Fuentes

• http://www.vitutor.net/2/9/inecuaciones_fraccionarias.html
• http://www.cidse.itcr.ac.cr/revistamate/.../inecuaciones13/index.ht
• http://www.cidse.itcr.ac.cr/revistamate/SoftDidactico/inecuaciones13/index.html
• http://www.algebra.itgo.com/problemas_sobre_ecuaciones_fraccionara
• http://www.scribd.com/doc/4563147/Tema-II-Ecuaciones-e-Inecuaciones