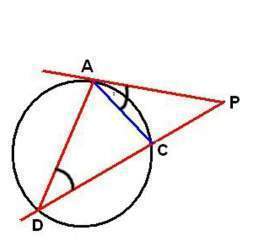
Relación entre una secante y una tangente
| ||||
Definición: La recta que tiene solamente un punto en común con una circunferencia se la llama recta tangente a la Circunferencia, en este caso la recta y la circunferencia tiene un punto en común: el resto de los puntos de la recta son exteriores a la circunferencia y el punto común a la recta y al Circunferencia recibe el nombre de Punto de tangencia
Teorema
Teorema: Si desde un punto exterior a una circunferencia se trazan una tangente y una secante, el segmento de tangente entre ese punto y el de contacto es medio proporcional entre los segmentos de secante comprendidos entre el punto y las intersecciones de la secante con la circunferencia
Hipotesis
PA tangente en A a la circunferencia y PD secante a la circunferencia
Tesis
PD : PA = PA : PC
Demostración
Trazando AC Y AD en la figura Demostremos que ∆PAD y ∆PAC son semejantes ∠P es común para ambos triángulos ∠ADP = ∠CAP Por se ángulos inscrito y semiinscrito que le corresponde el mismo arco AC Por tanto se verifica que ∆PAD y ∆PAC son semejantes por tener dos ángulos respectivamente iguales Luego estableciendo la proporcionalidad entres los lados homólogos se cumple: PD : PA = PA : PC
Nota: Al segmento de tangente trazada desde un punto, comprendido entre este y el de contacto, se le suele llamar Longitud de la tangente y es muy corriente ver este teorema enunciado de esta manera: Si desde un punto exterior a una circunferencia se trazan una tangente y una secante, la tangente es la media proporcional entre la secante y un segmento externo
Fuente
[Matemática Cuarto curso. Geometría.de Antonio Paz]
Enlace externo
[|http://usuarios.multimania.es/algetrico/id29.htm] Relación_entre_los_segmentos_de_dos_Secantes