Construcción y Cálculo del segmento ÁUREO de un segmento dado

Segemnto Áureo
Información sobre la plantilla
Áureo.jpg


SegmentoÁUREO

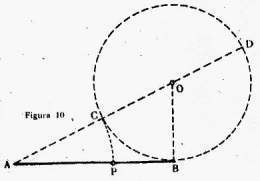
Sea AB (fig 10) el segmento dado. 



En unos de los extremos  levantésmosle  una perpendicular y tomemos sobre ella
el segmento BO = ½ AB.

Con centro en O y radio OB describimos una circunferencia y tracemos la secante AD pasando por el centro O. Con centro en A y radio AC cortemos a AB en P.El segmento AP es el segmento áureo de AB. En efecto, como desde A hay trazadas una tangente y una secante a la circunferencia, se verifica AD:AB = AB :AC Por una propiedad de las proporciones 

     (AD – AB)/AB = ( AB – AC )/AC

pero AD – AB = AD – CD = AC, Puesto que siendo el radio de la circunferencia igual a ½ AB. Además AB – AC = AB – AP = PB, y por la proporcion anterior se conviente en: 

AC : AB = PB : AC

Invirtiendo las razonnes y teniendo en cuenta que AC = AP, resulta 

  AB : AP = AP : PB

lo que justifica la construcción anterior, puesto que P divide a AB en media y extrema razón, de acuerdo con la definición.

OBSERVACIÓN: Además de P, existe sobre la recta que contiene a AB, otro punto a la izquierda de A que también divide en media y extrema razón. Para obtenerlo basta hacer en A y con radio AD cortar la prolongación de BA

CALCULO DEL SEGMENTO ÁUREO

Sea P = x, el segmento áureo de un segmento dado a. Calculemos x en función de a. Fig 11

ÁUREO1.jpg

se tiene que a : x = x : (a – x) resolviendo la ecuación resulta: x2 = a(a – x) de donde x2 + ax – a2 = 0 

las dos raices son
x = - a/2 ± √(a2/4 + a2)

separando las raices 

x1 = - a/2 + a/2√(5) = a/2 (-1 + √(5))

x2 = - a/2 - a/2√(5) = a/2 (-1 - √(5))

considerando unicamente el valor positivo de la raíz, se obtiene para el segmento áureo la longitud siguiente x = a/2 *(√(5) -1) Aproximadamente 

x =  a/2 *(2,236 -1) =a/2 *1,236 = 0,618a

como 0,618 > ½ resulta 

         r >  ½ a

luego el segmento áureo de un segmento dado es siempre mayor que la mitad del segmento.

Fuente

Matemática Cuarto curso. Geometría.de Antonio Paz

Enlace externo

http://rt000z8y.eresmas.net/El%20numero%20de%20oro.htm http://personal.telefonica.terra.es/web/imarti22/actividades/actividades/teano/marco_teano2.htm http://mx.answers.yahoo.com/question/index?qid=20100909191920AAl5d2N http://harapos.blogspot.com/2005/07/segmento-ureo.html

Obtenido de «https://www.ecured.cu/index.php?title=Construcción_y_Cálculo_del_segmento_ÁUREO_de_un_segmento_dado&oldid=766727»