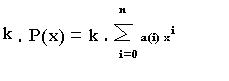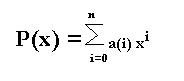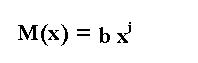Multiplicación de polinomios
| ||||||
Multiplicación de polinomios. Se deben multiplicar todos los monomios de unos, por todos los del otro y sumar los resultados.
Sumario
Multiplicación de un número por un polinomio
Partiendo de un polinomio P(x), el producto de este polinomio por un escalar k, es un polinomio k P(x), en el cual cada uno de los coeficientes de los del polinomio se ha multiplicado por k.
Si el polinomio es:

Dando lugar a:
Ejemplo:
P(x) = 3x2 + 4 x3 – 6x4
Lo multiplicamos por 5
P(x) = 5 . (3x2 + 4 x3 – 6 x4)
Obteniendo como resultado
5 . P(x) = 15 x2 + 20 x3 – 30 x4
Multiplicación de un polinomio por un monomio
Partiendo de un polinomio P(x), y un monomio M(x), el producto P(x)*M(x) es un polinomio que resulta de multiplicar los coeficientes del polinomio por el del monomio, y sumar a los grados del polinomio el del monomio, veamos: Si el polinomio es:
y el monomio es:
el producto del polinomio por el monomio es:
Agrupando términos:
El producto de exponentes de la misma base, es la base elevada a la suma de los exponentes:
Ejemplo:
3x2 · (2x3 − 3x2 + 4x − 2)
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
3x2 · (2x3 − 3x2 + 4x − 2)= 6x5− 9x4 + 12x3 − 6x2)
Multiplicación de dos polinomios
Dados dos polinomios P(x) de grado n y Q(x) de grado m, el producto de estos dos polinomios P(x) * Q(x) que será un polinomio de grado n + m, así si:
Entonces:
Obteniendo como resultado al aplicar las propiedades correspondientes:
Ejemplo:
P(x) = 2x2 − 3
Q(x) = 2x3 − 3x2 + 4x
Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.
P(x) · Q(x) = (2x2 − 3) · (2x3 − 3x2 + 4x) = 4x5 − 6x4 + 8x3 − 6x3 + 9x2 − 12x
Se suman los monomios del mismo grado.
= 4x5 − 6x4 + 2x3 + 9x2 − 12x
Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
También podemos multiplicar polinomios de siguiente modo: