Polígono regular
| ||||||
Polígono regular. En Matemáticas y Geometría son las figuras poligonales convexas que tienen todos sus lados y ángulos interiores iguales.
Al polígono de n lados se le llama también n-ágono regular.
Otra característica de importancia capital es el hecho de que también sus ángulos interiores y exteriores sean congruentes, lo cual facilita enormemente el cálculo del perímetro, área; partes integrantes, aspectos que han conllevado a lo largo del desarrollo de la geometría y usar en el cálculo de otras superficies más complejas; en tal circunstancia se ven como casos más particulares, los n-ágonos. Además sus apotemas son iguales, y los radios de los círculos inscritos o circunscritos pueden calcularse, aun trigonométricamente.
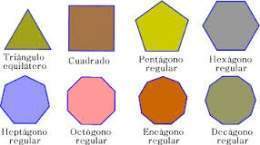
El polígono regular de menos lados es el triángulo equilátero, le siguen los cuadrados, pentágonos regulares, etc.
No debe confundirse con el concepto de polígono equilátero (polígonos cuyas aristas tienen todas igual longitud) pues entre estos los hay que son convexos pero no regulares como es el caso del rombo y otros que tienen concavidades.
Sumario
Definiciones
Se dice que un polígono es regular si y solo si sus lados y ángulos internos son iguales entre sí.
| Descripción de los elementos de un polígono regular |
|---|
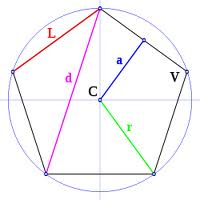
|
|
Ejemplos
A continuación se muestra una tabla con algunos polígonos regulares y algunos de sus valores generales.
| N | Nombre | Figura | Ángulos centrales | Ángulos interiores | Perímetro |
|---|---|---|---|---|---|
| 3 | triángulo equilátero | 120o | 60o | 3l | |
| 4 | cuadrado | 90o | 90o | 4l | |
| 5 | pentágono | 72o | 108o | 5l | |
| 6 | hexágono o exágono | center|60px | 60o | 120o | 6l |
| 7 | heptágono | 51,428571o | 128,571428o | 7l | |
| 8 | octágono | 45o | 135o | 8l | |
| 9 | nonágono | 40o | 140o | 9l | |
| 10 | decágono | 36o | 144o | 10l | |
| 11 | endecágono o undecágono | 32.72o | 147.27o | 11l | |
| 12 | dodecágono | 30o | 150o | 12l | |
| 50 | quincuágono | 7,2o | 172,8o | 50l |
Puede apreciarse como al aumentar el número de lados el polígono tiende a asemejarse a un círculo.
Propiedades
- Todo polígono regular es equilátero y equiángulo.
- No son polígonos regulares ni el rombo ni el rectángulo no cuadrados, aun siendo el primero equilátero y el segundo, equiángulo.
- Si dividimos una circunferencia en n partes iguales, donde n no menor que 3, y unimos consecutivamente los puntos de división mediante segmentos se obtiene un n-ágono regular inscrito.
- Si dividimos una circunferencia en n partes iguales, donde n no menor que 3, y trazamos consecutivamente por los puntos de división rectas tangentes (cada una corta a dos de ellas) que se intersecan, se obtiene un n-ágono regular circunscrito. [1]
Cálculo
Los polígonos regulares tienen una serie de propiedades que hacen que se facilite enormente el cálculo de sus elementos conformantes además del perímetro y área.
Las variables que aparecen han sido referidas desde el epígrafe de definiciones
Elementos componentes
La definición de los n-ágonos regulares permiten que existan estrechas relaciones entre sus componentes geométricos de manera que si se conocen algunos de ellos puede obtenerse el resto.
- Relación algebraica de r, h y l: 4r2=4h2+l2.
- Amplitud de los ángulos interiores:
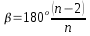
- Amplitud de los ángulos centrales:
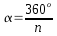 .
. - Amplitud de los ángulos exteriores:
 .
.  .
. .
.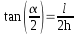 .
.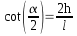 .
.
Perímetro
Evidentemente la forma más trivial de obtener el perímetro de un n-ágono regular es conociendo la longitud l de uno de sus lados, en cuyo caso:
- Ln = nl
En función del radio de la circunferencia circunscrita r la fórmula se ajusta a:
Área
Para determinar el área de un n-ágono regular, lo más práctico es subdividirlo en triángulos, trazando los radios r de la circunferencia circunscrita hacia cada uno de los vértices, que resulta en n triángulos isósceles iguales (los radios son iguales y por definición, las aristas son congruentes) entre sí, de manera que si se conoce el área AT de uno de esos triángulos puede calcularse la superficie general mediante:
- An=nAT
Mientras tanto, AT puede determinarse mediante la fórmula general del área de triángulos:
Resumiendo:
En otra situación si se tuviese el radio de la circunferencia circunscrita r, la expresión total de superficie queda:
O esta otra que depende de la apotema y el ángulo central:
Áreas de las circunferencias circunscrita e inscrita
Si se conoce la longitud l del n-ágono regular pueden calcularse los valores de las superficies correspondientes a las circunferencias circunscrita e inscrita.
| Tipo | Área | Perímetro |
|---|---|---|
| Circunferencia inscrita | 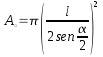 |
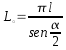
|
| Circunferencia circunscrita |
Diagonales
Siendo n el número de lados del polígono; n no menor que 3
- Número de diagonales
- Nd = n(n-3)/ 2
- Número de intersecciones de las diagonales
- NId = n(n-1)(n-2)(n-3)/ 24 [2]
Representación gráfica
La representación gráfica de n-ágonos regulares ha sido de interés particular de la geometría, arquitectura, diseño, dibujo técnico, artes plásticas, religión, generación de gráficos por computadora tanto 2D como tridimensionales y otras muchas, por tanto a lo largo del tiempo se han desarrollado métodos de toda clase para su obtención.
De gran interés desde las grandes culturas de la Antigüedad fue la obtención de los mismos con instrumentos sencillos como regla y compás, consiguiéndose con cierta celeridad la construcción de los polígonos regulares de 3, 4, 5, 6, 8 y 15 lados con el alto desarrollo geométrico alcanzado en la Grecia de Euclides, aunque formas similares se hayan en textos clásicos de la Antigua India, China y Egipto, además de las tabletas cuneiformes de Mesopotamia.
Sin embargo había figuras que se resistían a la construcción con regla y compás como el heptágono que más de 2 mil años después se probraría la incapacidad de obtenerlo solo con regla y compás.
A los polígonos regulares que pueden obtenerse con estos instrumentos se les conoce como polígonos construibles. La idea central es lograr dividir un círculo en n secciones iguales, fenómeno llamado ciclotomía del griego cyclos (círculo) y tomo (dividir, divisible).
En 1796 Gauss demuestra que es posible también construir con regla y compás el heptadecágono (n-ágono regular de 17 lados) y cinco años después había establecido una condición suficiente para que un polígono regular fuese construible estableciendo una asociación entre la cantidad de lados y los llamados actualmente números primos de Fermat.
Evidentemente, la geometría analítica presentaba soluciones algebraicas más simples. La idea es la misma que una ciclotomía de n partes iguales que si se asume que el círculo de radio r tiene su origen en el centro de coordenadas (0;0) los vértices del n-ágono regular se ubican en los puntos:
Si se quiere una versión más general que incluya rotar en un ángulo ![]() .
.
El traslado a otra coordenada (x,y) del centro solo requiere la adición es dichos valores a todas las coordenadas de los vértices:
Importancia
El conocimiento y propiedades de estas figuras geométricas trasciende el terreno de las matemáticas donde de por sí han constituido una fascinación tanto abstracta como estética por la simpleza y regularidad armónica de sus formas, para alcanzar a otras áreas del conocimiento y prácticas de la Humanidad.
Es fácil notar que un polígono regular entre más lados tiene más se asemeja a un círculo, y que su infinitación de hecho constituye al círculo. Este resultado ayudó en la antigüedad a la obtención de aproximaciones del número pi mediante el método exhaustivo donde se iba tomando la medida de las longitudes de n-ágonos regulares unitarios cuyos.
Sirven también para el cálculo de superficie y volumen de figuras más complejas inscribiendo n-ágonos regulares de fórmulas conocidas en ellos. Una de los métodos de expresión visual de grafos tiene por base la ciclotomía de los polígonos regulares.
En la naturaleza existen materiales, partículas, moléculas, ondas que tienen el aspecto de estas figuras o puede modelarse su comportamiento mediante las fórmulas que rigen a los n-ágonos. Ejemplo de esto son las formas hexagonales de los cristales de hielo en los copos de nieve o las moléculas de grafito y benzeno.
El dibujo, las artes plásticas y el diseño hacen uso de estas con diversos propósitos estéticos, expresivos o conceptuales pues algunas de estas figuras forman parte de la cultura general o de naciones, grupos étnicos o religiones asociando simbólicamente sus formas a ideas, conceptos, fenómenos, abstracciones, movimientos, tendencias, modas, etc.
La generación de imágenes por computadora (GIC, CGI en inglés), videojuegos, edición AVID y los gráficos 3D casi siempre tienen a lo más elemental polígonos o poliedros cuyas propiedades tan cómodas favorecen la velocidad de cálculo para una obtención poco costosa en términos de poder de cálculo de cada cuadro, de modo que se cumpla en tiempo real la siempre deseable propiedad lo que ve es lo que obtendrá (WYSIWYG, por su equivalente en inglés).
Notas
Fuentes
- I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial MIR, Moscú. 1973.
- K. Ríbnikov. Historia de las Matemáticas. Editorial Mir, Moscú. 1987.
- Artículo. Polígono regular. Disponible en: "es.wikipedia.org". Consultado: 20 de marzo de 2012.