Polinomio
| ||||
Polinomio. Es una expresión constituida por un conjunto finito de variables (no determinadas o desconocidas) y constantes (números fijos llamados coeficientes), utilizando únicamente las operaciones aritméticas de suma, resta y multiplicación, así como exponentes enteros positivos. En otras palabras, es una combinación lineal de productos de potencias enteras de una o de varias indeterminadas.
Sumario
Definición
En general la suma algebraica de varios monomios recibe el nombre de polinomio.
Se consideran expresiones algebraicas aquellas donde los números y las variables aparecen relacionados por cualquiera de las operaciones de cálculo.
Ejemplo: 3x2+y; (c-d)*2m son expresiones algebraicas.
Valor numérico de una expresión algebraica
Si en una expresión algebraica se sustituyen las variables por números y se efectúan las operaciones indicadas, el valor resultante (si existe) recibe el nombre de valor numérico de la expresión algebraica.
Grado de un monomio
Se denomina grado de un monomio (en el cual sus factores literales aparezcan con exponentes enteros no negativos), a la suma de los exponentes de las variables que contengan. Ejemplo: a) 3x es de grado 1. b) 2a2 es de grado 2. c) rst es de tercer grado d d) 4m3n es de cuarto grado En general, los términos en que solo aparece el coeficiente numérico tienen grado cero. Nota: A veces se considera el grado de un monomio con respecto a algunas de las variables que contienen. Por ejemplo el monomio 4m3n es de tercer grado con respecto a la m y de primer grado con respecto a la n.
Grado de un polinomio
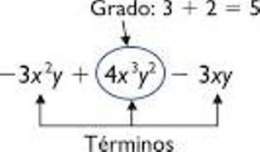
Se denomina grado de un polinomio al mayor de los grados de los términos (monomios) que lo componen.
Ejemplo:
a) 2x + 3 es de primer grado.
b) 3a2 + 2a – 8 es de segundo grado.
c) 1 + 3b – b3 + b2 es de tercer grado
Nota: El grado de un polinomio que contenga más de una variable también puede considerase con respecto a una de ellas.
Operaciones con polinomios
- Adición de polinomios.
- Sustracción de polinomios.
- Eliminación e introducción de paréntesis.
Adición de polinomios
Para adicionar polinomios se escriben uno a continuación del otro, conservando cada término su signo y reduciendo términos semejantes en caso de que existan.
Ejemplo: Para adicionar 2a + b y 7a – 2b
2a + b + 7a – 2b = 9a – b
Sustracción de polinomios
Para sustraer un polinomio de otro se escribe el minuendo tal y como está y a continuación el sustraendo cambiándole el signo a cada uno de sus términos, luego se reducen los términos que sean semejantes.
Ejemplo: (5x + 2y) – (3x – y) = 5x + 2y – 3x + y= 2x + 3y
Eliminación e introducción de paréntesis
Eliminación
- Todo paréntesis precedido por el signo ”+” puede eliminarse dejando los términos del polinomio incluido en él con sus propios signos.
- Todo paréntesis precedido por el signo “-“puede eliminarse siempre que se cambie el signo del polinomio incluido en él.
Ejemplo: 7x2 + (-3xy – y2) – (2x2 + xy – 3y2) = 7x2 – 3xy – y2 – 2x2 – xy + 3y2
= 5x2 - 4xy + 2y2
Introducción
- Si el paréntesis que se introduce está precedido por el signo “+”, los términos que se incluyen en él conservan sus propios signos.
- Si el paréntesis que se introduce está precedido por el signo “-“, se le cambia el signo a los términos que se incluyen en él.
Multiplicación de polinomios
Para multiplicar dos polinomios se aplica también la propiedad distributiva. De esta forma se obtiene un nuevo polinomio cuyos términos son los productos de cada término del primer polinomio por cada término del segundo polinomio.
Ejemplo: (2a + b)(3 a - 4b) = 2a * 3a – 2a * 4b + b * 3a – b *4b
= 6a2 - 8ab + 3ab – 4b2=6a2 - 5ab – 4b2
División de polinomios
Para dividir un polinomio por otro polinomio
- El dividendo y el divisor deben ordenarse en potencias decrecientes de una misma variable.
- Se divide el primer término del dividendo por el primer término del divisor, obteniéndose el primer término del cociente.
- Este primer término del cociente se multiplica por el divisor y el producto resultante se sustrae del dividendo; de esta forma se obtiene el resto.
- Si este resto es de mayor o igual grado que el divisor (atendiendo a la variable respecto a la cual se ordenaron los polinomios), lo consideramos como el nuevo dividendo y se repite así el proceso hasta obtener un resto de menor grado que el divisor, el cual será el resto de la división.
Fuentes
- Matemática 8vo grado. Editorial Pueblo y Educación 1990.
- Polinomios
- Calcular polinomios
- Diferentes operaciones con polinomios