Diferencia entre revisiones de «Proporcionalidad de segmentos»
m (Texto reemplazado: «<div align="justify">» por «») |
|||
| (No se muestran 3 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | {{Definición|nombre= Proporcionalidad de Segmentos | + | {{Definición |
| + | |nombre=Proporcionalidad de Segmentos | ||
| + | |imagen= | ||
| + | |tamaño= | ||
| + | |concepto=es la conformidad o proporción de la (igualdad de dos razones.) | ||
}} | }} | ||
| − | + | '''Proporcionalidad de segmentos'''. Es la relación de igualdad que existe entre dos razones. Por ende, se entenderá entonces que dos razones proporcionales son dos razones iguales. | |
| − | |||
| − | |||
== Definición == | == Definición == | ||
| − | |||
Llamamos proporcionalidad de segmentos a la aplicación existente entre el conjunto de cantidades de longitud en sí mismo, de tal forma que la aplicación sea biyectiva, conserve el orden, la igual y además mantenga la correspondencia con la operación de la suma. | Llamamos proporcionalidad de segmentos a la aplicación existente entre el conjunto de cantidades de longitud en sí mismo, de tal forma que la aplicación sea biyectiva, conserve el orden, la igual y además mantenga la correspondencia con la operación de la suma. | ||
[[Imagen: 12-244x300.png|left||165px|]] | [[Imagen: 12-244x300.png|left||165px|]] | ||
| − | |||
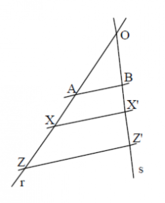
Teorema fundamental de proporcionalidad: Dadas dos rectas r y s que se cortan en el punto O y dadas dos longitudes a y b sobre cada una de las rectas respectivamente de tal forma que determinan los segmentos OA=a y el OB=b, como podemos observar en la imagen. Trazando la recta que une los puntos A y B y rectas una recta paralela a esta que corta a las rectas r y s en el punto X y X’ respectivamente, entonces al segmento OX se le hace corresponder el segmento OX’. | Teorema fundamental de proporcionalidad: Dadas dos rectas r y s que se cortan en el punto O y dadas dos longitudes a y b sobre cada una de las rectas respectivamente de tal forma que determinan los segmentos OA=a y el OB=b, como podemos observar en la imagen. Trazando la recta que une los puntos A y B y rectas una recta paralela a esta que corta a las rectas r y s en el punto X y X’ respectivamente, entonces al segmento OX se le hace corresponder el segmento OX’. | ||
| Línea 55: | Línea 55: | ||
*'''Cuaterna armónica: ''' Dados cuatro puntos alineados A, B, X y X’, diremos que forman una cuaterna armónica siempre y cuando se cumpla la siguiente razón de proporcionalidad entre los segmentos: XA/XB=X’A/X’B | *'''Cuaterna armónica: ''' Dados cuatro puntos alineados A, B, X y X’, diremos que forman una cuaterna armónica siempre y cuando se cumpla la siguiente razón de proporcionalidad entre los segmentos: XA/XB=X’A/X’B | ||
| − | [ | + | == Fuentes == |
| + | *PROPORCIONALIDAD DE SEGMENTOS. TEOREMA DE THALES [https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=27&ved=2ahUKEwjiwa6lxv_fAhUG1VkKHfL3D_oQFjAaegQIBRAC&url=https%3A%2F%2Fwww.sectormatematica.cl%2Fmedia%2FNM2%2FNM2_Teorema_de_thales_2.doc&usg=AOvVaw0XlPUdabQKnkM6miw86dus]. Consultado. 21 de enero del 2019 | ||
| − | + | [[Category:Matemáticas]] | |
| − | |||
última versión al 22:45 12 ago 2019
| ||||
Proporcionalidad de segmentos. Es la relación de igualdad que existe entre dos razones. Por ende, se entenderá entonces que dos razones proporcionales son dos razones iguales.
Definición
Llamamos proporcionalidad de segmentos a la aplicación existente entre el conjunto de cantidades de longitud en sí mismo, de tal forma que la aplicación sea biyectiva, conserve el orden, la igual y además mantenga la correspondencia con la operación de la suma.
Teorema fundamental de proporcionalidad: Dadas dos rectas r y s que se cortan en el punto O y dadas dos longitudes a y b sobre cada una de las rectas respectivamente de tal forma que determinan los segmentos OA=a y el OB=b, como podemos observar en la imagen. Trazando la recta que une los puntos A y B y rectas una recta paralela a esta que corta a las rectas r y s en el punto X y X’ respectivamente, entonces al segmento OX se le hace corresponder el segmento OX’.
Por tanto se cumple la siguiente razón de proporcionalidad.
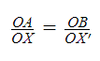
Propiedades
En todas las razones de proporcionalidad entre segmentos se cumplen las siguientes propiedades:
- El producto de medios es igual al producto de extremos:
- Si cambiamos el orden de los extremos obtenemos la misma razón de proporcionalidad:
- Análogamente al apartado anterior, cuando cambiamos los medios también obtenemos la misma razón de proporcionalidad:
- Si cambiamos el orden de las fracciones no cambia la proporcionalidad:
- Si invertimos los numeradores y los denominadores en cada fracción la proporcionalidad no es la misma:
- Si sumamos o restamos a cada antecedente su consecuente obtenemos otra proporción
Proporciones Notables
Vamos a ver algunos de los ejemplos y las proporciones más notables.
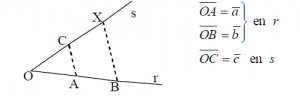
- Cuarto proporcional: Dados tres segmentos a, b y c llamamos cuarto proporcional x, de los segmentos a, b y c, como el único segmento que verifica la siguiente relación: a/b=c/x.
Como podemos ver de forma geométrica, si trazamos la paralela a la recta AC que pasa por B obtenemos el punto de corte con la recta s, de tal forma que el segmento OX es el cuarto proporcional buscado. Como se ve, trazando la paralela a la recta AC que pasa por B obtenemos un punto. X de corte con la recta s, tal que OX = x es el segmento buscado, el cuarto proporcional.
- Tercero proporcional: Dados dos segmentos a y b cualesquiera, llamamos tercero proporcional de a y b al segmento x tal que: a/b=b/x.
La construcción es similar al cuarto proporcional considerando que c=b.
- Cuaterna armónica: Dados cuatro puntos alineados A, B, X y X’, diremos que forman una cuaterna armónica siempre y cuando se cumpla la siguiente razón de proporcionalidad entre los segmentos: XA/XB=X’A/X’B
Fuentes
- PROPORCIONALIDAD DE SEGMENTOS. TEOREMA DE THALES [1]. Consultado. 21 de enero del 2019