Diferencia entre revisiones de «Tareas integradoras de Matemática y Física»
| Línea 30: | Línea 30: | ||
[[Image:Grafico fisica matematica.JPG|thumb|center|450x450px|]] | [[Image:Grafico fisica matematica.JPG|thumb|center|450x450px|]] | ||
a)Completa el espacio en blanco: A los 5 s el cuerpo alcanza una velocidad de ______ | a)Completa el espacio en blanco: A los 5 s el cuerpo alcanza una velocidad de ______ | ||
| + | |||
b)Selecciona la respuesta correcta situando una (x) sobre la raya, solo es correcta una de las opciones dadas. | b)Selecciona la respuesta correcta situando una (x) sobre la raya, solo es correcta una de las opciones dadas. | ||
*La velocidad se mantuvo constante durante: | *La velocidad se mantuvo constante durante: | ||
Revisión del 14:51 31 jul 2013
| ||||||
Esta Tareas integradoras fortalece el desarrollo de habilidades Matemática desde la asignatura Física. En este proceso se parte de las diferentes concepciones que sobre el tema de la interdisciplinariedad se debaten en la contemporaneidad educativa; además de establecer los interobjetos existentes entre Física y Matemática, elemento que sentaron las bases para una elaboración efectiva de las tareas integradoras.
Sumario
Estructura de la Tarea
Para que el proceso de enseñanza–aprendizaje se desarrolle acorde con las exigencias actuales es necesario dedicar especial atención al trabajo metodológico, con énfasis en la utilización de métodos y procedimientos que activen el pensamiento lógico de los estudiantes, es decir que conviertan la actividad de aprender en algo placentero, estimulante y motivador; por tanto en el propio trabajo metodológico como en la clase se deben concebir tareas integradoras que propicien el vínculo entre los contenidos de las asignaturas Física y Matemática.
- En la implementación de la propuesta se debe transitar por las siguientes fases o etapas.
- La primera etapa consiste en la aplicación del diagnóstico, realizado con la finalidad de obtener información que permita transformar la situación real en la deseada; es necesario el dominio por parte de los profesores del departamento de los conocimientos precedentes.
- En la segunda etapa se define la contradicción interna, que está dada por la pobre preparación de los docentes para determinar los nexos esenciales de las asignaturas Física y Matemática, lo que dificulta la elaboración de tareas integradoras.
- La tercera etapa consiste en la elaboración de un conjunto de tareas integradoras para propiciar el vínculo entre las asignaturas Física y Matemática. Las tareas aparecen relacionadas a continuación.
- La cuarta etapa consiste en la socialización de la propuesta de tareas integradoras en el colectivo de profesores.
- Análisis crítico de las tareas
- Valoración de las recomendaciones metodológicas para su instrumentación.
- Trazado de acuerdos y líneas de trabajo para su puesta en práctica.
- La quinta etapa es la instrumentación de las tareas integradoras en la práctica pedagógica. Es recomendable señalar que para el cumplimiento de esta fase se requiere de un dominio de los elementos teórico–metodológico relacionados con este tipo de tareas, así como de los nexos existentes entre ambas ciencias.
Requisitos para desarrollar las tareas integradoras
- Cada profesor debe dominar su disciplina. (Física)
- Dominar la disciplina con la que va a potenciar las relaciones interdisciplinarias. (Matemática)
- Estudiar los programas de las disciplinas con las que se van a potenciar las relaciones interdisciplinarias. (Física y Matemática)
- Establecer los nexos para lograr los objetivos propuestos entre las diferentes disciplinas. (Física y Matemática)
- Tiene que existir comprensión e interés por el docente para llevar a cabo la interdisciplinariedad. (Profesor de Física y Matemática)
- Es requisito indispensable un eficiente trabajo metodológico en el departamento docente. (Ciencias Exactas)
- Los órganos de dirección tienen que desempeñar un papel predominante en la dirección del trabajo metodológico. (Consejo de dirección)
Ejemplo
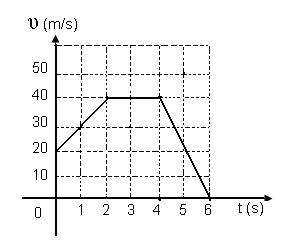
En el sistema de coordenadas se representa la variación de la velocidad de un móvil en distintos intervalos de tiempo.
a)Completa el espacio en blanco: A los 5 s el cuerpo alcanza una velocidad de ______
b)Selecciona la respuesta correcta situando una (x) sobre la raya, solo es correcta una de las opciones dadas.
- La velocidad se mantuvo constante durante:
- Ø ____4 s
- Ø ____ 2 s
- Ø ____ 6 s
c) La ecuación de la función lineal que describe el aumento de la velocidad es:
- Ø _____ ν= -10t + 20
- Ø _____ ν= 10(t + 2)
- Ø _____ ν= 30t + 20
- Ø _____ ν= 20t + 10
d) Escriba las ecuaciones de los movimientos de la forma y=mx+ n.
Recomendaciones metodológicas
Los contenidos se trabajan en la unidad # 2 de ambas asignaturas y son similares. En estos ejercicios se trabajan los contenidos del ejercicio anterior, su diferencia radica en que poseen un grado mayor de complejidad porque el estudiante tiene que poner en práctica todo lo que estudió en la función lineal y vincularla con los movimientos rectilíneos. Ambos contenidos se imparten en similares tiempos, por lo que los profesores pudieran acordar una misma terminología para darle tratamiento.
Este ejercicio parece común a los que se trabajan en clase, la diferencia está en la terminología que emplee el profesor de Física para explicarlo.
Las funciones lineales se representan por la ecuación de la forma y = mx + n.
- Si m>0 la función es creciente, si la ∆ν >0 es un MRUA.
- Si m < 0 la función es decreciente, si la ∆ν < 0 es un MRUR.
- Si m = 0 la función es constante, si la ν es constante el MRU, en este caso se puede analizar que la a = 0 demostrándolo con la ecuación para determinar la pendiente.
Para resolver el inciso c del ejercicio 11 y 13 se puede partir del siguiente análisis. La ecuación de la función lineal se puede obtener si se conoce:
- La pendiente m y un punto P(x0; y0)
- Dos puntos P1(x1;y1) y P2 (x2; y2), con los dos puntos se obtiene la m y se procede como en el caso anterior. Este último es el que hay que utilizar para determinar la ecuación del ejercicio anterior con los puntos P1 (t1;ν1) y P2 (t2; ν2), se obtiene la pendiente m= ν2 –ν1 ⁄ t2- t1, con un punto y la m puede sustituir en la ecuación ν = ν0 + at, a=m y νo es el intercepto con el eje de las ordenadas.
- Para determinar cuando el cuerpo se encontraba en reposo se iguala la ecuación a cero y se determina para qué valor de t la velocidad es cero.
Fuente
- Master en Ciencias de la Educación:Yanelis Marzo Herrera. Profesora de Matemática.
- VELÁZQUEZ ÁVILA, RENÉ A. El perfeccionamiento del modo de actuación Interdisciplinario en docente del Área de Ciencias Naturales de la enseñanza Preuniversitaria.--2005.---210p. Tesis (Doctor en Ciencias de la Educación) ISP “José de la Luz y Caballero” Holguín, 2005.
- MAESTRÍA EN CIENCIAS DE LA EDUCACIÓN. Fundamentos de la investigación educativa. Tabloides Ι y ΙΙ.∕ Addine, Fátima… et.al. – La Habana: Ed. Pueblo y Educación, 2005.