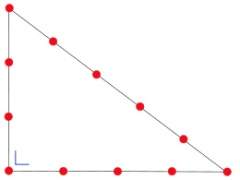
Triángulo Sagrado Egipcio
Triángulo sagrado egipcio o Triángulo egipcio. Es el nombre moderno dado a un triángulo rectángulo cuyos lados tienen las longitudes 3, 4 y 5, o sus medidas guardan estas proporciones. Es el triángulo rectángulo más fácil de construir y, posiblemente, se utilizó para obtener ángulos rectos en las construcciones arquitectónicas desde la más remota antigüedad. El triángulo rectángulo similar, de 15, 20, 25 codos egipcios, se empleó en el Antiguo Egipto y fue llamado «Isíaco» (de la diosa Isis).
Sumario
- 1 Origen del nombre
- 2 Propiedades
- 2.1 Ángulos agudos
- 2.2 Similitudes con otros triángulos rectángulos
- 2.3 Propiedades musicales y de proporciones
- 2.4 Propiedades aritmético-geométricas
- 2.5 Área y relación a los cubos de sus lados
- 2.6 Propiedades relacionadas con medidas angulares y astronómicas
- 2.7 Propiedades relacionadas con las secciones de las pirámides de Giza
- 3 El triángulo sagrado egipcio en la Gran Pirámide
- 4 Fuentes
Origen del nombre
Aunque no se conoce de donde proviene su nombre, se sabe que los antiguos tenían una geometría sagrada que era mantenida como doctrina secreta por los sacerdotes, que tuvo su origen en Babilonia y ejerció influencia tanto en el Antiguo Egipto como en la Antigua Grecia. Cualquiera haya sido la razón, este triángulo tiene numerosas propiedades notables.
Propiedades
Este triángulo, tan conocido y utilizado para obtener ángulos rectos, tiene muchas propiedades, tanto aritméticas o geométricas, como de coincidencias con períodos astronómicos, tales como el período de revolución sinódica de un planeta visible a simple vista o los múltiplos mínimos comunes de varios de esos períodos. Pero, después de cinco mil años de uso y estudio la información está tan dispersa que es casi imposible dar una lista completa del lugar en el que está cada afirmación.
Ángulos agudos
La amplitud de sus ángulos agudos es: 36º 52' 11,631 525 038 476 668 680 205 212 736 278 4..." y 53º 7' 48, 368 474 961 523 331 319 794 787 263 721 6..."
Similitudes con otros triángulos rectángulos
Como todo triángulo rectángulo cumple la siguiente ecuación: x² + y² = z² (Teorema de Pitágoras); x = k(m² - n²), y = k(2mn), z = k(m² + n²), donde m y n son enteros positivos de distinta paridad (Ver: números pares e impares) con m > n y k es un entero positivo cualquiera. Si k = 1 tenemos todas las ternas primitivas y conservando m y n el producto por k cualquiera produce triángulos semejantes de ternas no primitivas, pues k es el divisor común. Algunos autores escriben y = k(mn) y dividen por 2 a los otros términos. Esto cambia las condiciones para m y n, que deben ser, entonces, ambos impares y primos entre sí para que las ternas sean primitivas.
Propiedades musicales y de proporciones
La escala diatónica mayor, debida a Pitágoras, comienza por la nota DO, que corresponde a la unidad, y a una frecuencia de 264 Hz (o ciclos por cada segundo); continúa RE: 9/8 = 27/24 - 297 Hz; MI: 5/4 = 30/24 - 330 Hz; FA: 4/3 =32/24 - 352 Hz; SOL: 3/2 = 36/24 - 396 Hz; LA: 5/3 = 40/24 - 440 Hz; SI, 15/8 = 45/24 - 495 Hz; DO, 2 = 48/24 - 528 Hz. La nota FA es la media armónica de la octava y SOL corresponde a sesqui veces el Do inicial (está sesqui-relacionada con el DO). Tanto el SOL como el DO que completa la octava representan a los catetos del triángulo sagrado egipcio (3/2, 2, 5/2), de igual forma en sus proporciones como en sus frecuencias. La hipotenusa del triángulo está en la octava siguiente y corresponde a la nota MI, 5/2 = 60/24 - 660 Hz (la proporción tomada desde el Do inicial de la anterior escala). Los triángulos (3/2, 2, 5/2), (3, 4, 5) y (396, 528, 660) son semejantes. El tercero es 264 veces el primero y 132 veces el segundo. Si dibujamos un triángulo sagrado egipcio, su recta de Euler parte del vértice del ángulo recto hasta el punto medio de la hipotenusa. El vértice del ángulo recto es el ortocentro y en la mitad de la hipotenusa se halla en circuncentro, que permite trazar la circunferencia que circunscribe al triángulo. Esa recta divide al triángulo en dos triángulos isósceles, cuyos ángulos no idénticos son, respectivamente: 106º 15' 36,7369499230466626395895745274432..." y 73º 44' 23,2630500769533373604104254725567...".
Propiedades aritmético-geométricas
Es el triángulo rectángulo diofántico –las medidas de los lados son números enteros– menor que pueda ser construido y, además, con un cateto y la hipotenusa números primos. Según estudió Fermat, las únicas hipotenusas primas son de la forma 4m + 1, donde m es un número natural. Cuando la terna que forman los lados tiene elementos primos entre sí se denomina terna primitiva. El doctor Tobías Dantzig, de la Universidad de Columbia, denominó "primarias" a las ternas primitivas con hipotenusa prima, aunque fue Fermat quien hizo la distinción entre hipotenusas primas y compuestas, dando todos los casos posibles de descomposición en suma de dos cuadrados para hipotenusas compuestas. Los catetos primos son de la forma 4m + 3, admitiendo en este caso el cero además de los números naturales para el valor asignado a m. Si A designa a un ángulo de una circunferencia con el vértice en el centro, y B y C a otros dos, tales que están en progresión aritmética de razón A/5, y A > B > C, los arcos rectificados de tales ángulos forman un triángulo rectángulo semejante al triángulo sagrado egipcio (3, 4, 5).
Área y relación a los cubos de sus lados
El triángulo sagrado egipcio tiene otras propiedades notables. Plutarco señala que su área es 6 (el primer número perfecto) y que el cubo de su área es igual a la suma de los cubos de sus lados. Platón se basa en esta igualdad para calcular un número que llama "nupcial". Platón fue discípulo de Sócrates, pero también toda su obra se halla impregnada de la filosofía de Pitágoras, aunque con algunas variantes propias de un alumno que aventaja a su lejano maestro. Los pitagóricos calificaban a los números pares como femeninos y a los impares como masculinos. La unidad no era considerada un número, sino el símbolo de la divinidad antes de la creación por la dualidad diferenciadora (negación-afirmación, luz-oscuridad, femenino-masculino, etc.), el primer número era el 2, considerado femenino, y el 3 era el primer número masculino. Para la escuela pitagórica el número 5 era el símbolo del matrimonio, la unión de los dos primeros números de distinto sexo. Platón, sin embargo, denomina "nupcial" al producto de tales números.
Propiedades relacionadas con medidas angulares y astronómicas
Los números 40 y 60 están sesqui-relacionados, pues 60 es una vez y media 40. El número 40 es el máximo común divisor de los mínimo común múltiplo de los períodos de las revoluciones sinódicas de los planetas visibles, tomados dos a dos, tres a tres o en su conjunto (ver: período orbital). Obtener el mínimo común múltiplo de la duración de dos revoluciones sinódicas permite saber en cuantos días se repite una observación en el cielo y, por tanto, sirve para elaborar calendarios.
Propiedades relacionadas con las secciones de las pirámides de Giza
Los números 40 y 60 en los tres lados de triángulos rectángulos: (24, 32, 40) = 8 (3, 4, 5) la hipotenusa es el tercer número de la terna. (9, 40, 41) (40, 42, 58) = 2 (20, 21, 29) (36, 48, 60) = 12 (3, 4, 5) (11, 60, 61) (60, 63, 87) = 3 (20, 21, 29) Muestran la relación de la segunda y la tercera pirámides de Giza.
El triángulo sagrado egipcio en la Gran Pirámide
En la hipótesis Φ, o sea, en la suposición de que la Gran Pirámide está construida basándose en el número áureo y a la propiedad enunciada por Herodoto de que «el cuadrado de su altura es igual a la superficie de una cara», el ángulo del vértice superior de la cara vale 63º 26' 5, 815 762 519 238 334 340 102 606 368 139 2..." Aunque este ángulo surge de la diagonal de un doble cuadrado y su complementario es igual a la inclinación del corredor de entrada, es posible construirlo uniendo el ángulo central de un octógono a la mitad del ángulo más agudo del triángulo sagrado egipcio -el que tiene por lados a la hipotenusa y el cateto proporcional a 4. Idéntico resultado se logra al unir el ángulo más agudo del triángulo sagrado egipcio al menor de los ángulos que forma la diagonal de un doble cuadrado con sus lados mayores. Respectivamente: 36,869897645844021296855612559093...º sumado a 26,565051177077989351572193720453...º es igual a 63,434948822922010648427806279547...º
Otro triángulo rectángulo notable en la cara de la Gran Pirámide
El triángulo rectángulo que resulta de cortar la cara de la pirámide por la apotema es el que tiene en su contorno los lados de un hexágono, un pentágono y un decágono, según un antiguo y conocido teorema geométrico. Esto es posible solamente si se acepta como hipótesis constructiva la sección áurea.
Diferencias de criterios
Hay dos posturas con respecto al criterio constructivo de la Gran Pirámide: una afirma que se intentó una cuadratura del círculo porque el semiperímetro dividido por la altura es próximo a π; la otra es la que contempla la afirmación de Herodoto y considera el número áureo. La primera es la que tiene el mayor número de adeptos, casi todos ellos basados en criterios empíricos y sin ser matemáticos profesionales (uno de ellos fue astrónomo y religioso). Los defensores de la hipótesis Φ son matemáticos, menos acostumbrados a las mediciones y más dispuestos a las consideraciones teóricas. Es imposible elegir mediante mediciones una u otra hipótesis, pues entre ambas hay una diferencia de 14,2 centímetros en la altura.
Considerando que la pirámide está truncada y que falta el revestimiento que fue depredado para la construcción de El Cairo, más los errores propios de toda construcción, en un monumento que tiene una base de más de 232 m de longitud, 14 centímetros se pierden dentro de la incertidumbre de las medidas (un error del 1 por mil en la base sería ligeramente superior a 23 cm, mientras que en la altura significaría 14,8 cm para la medida más grande que se obtuvo). Hay casi tantas medidas como medidores. Las medidas más admitidas tienen error inferior al decímetro.
El triángulo sagrado egipcio en el sarcófago de la Cámara del Rey
El paralelepípedo de la Cámara del Rey, también llamado sarcófago por algunos, aunque no hay prueba arqueológica de que haya sido tal, ni que la cámara fuera efectivamente la del rey, tiene propiedades remarcables de la geometría de los poliedros regulares y de la esfera. Entre las cosas más sencillas que se pueden mencionar se halla que es el único paralelepípedo recto rectángulo (ortoedro) que tiene una base igual a un doble cuadrado simultáneamente con un rectángulo diagonal igual a un doble cuadrado y otro de sus rectángulos diagonales es igual a la reunión de dos triángulos sagrados egipcios.