Ábaco neperiano

Ábaco neperiano Concepto: Ábaco inventado por John Napier para el cálculo de productos y cocientes de números

Ábaco. inventado por John Napier para el cálculo de productos y cocientes de números. También llamado ábaco rabdológico (del griego ραβδoς, varilla y λóγoς, tratado).

Historia

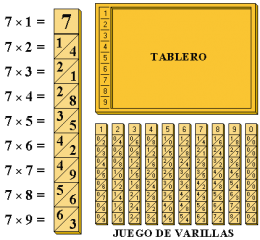
Napier publicó su invención de las varillas (virgŭla) en una obra impresa en Edimburgo a finales de 1617 titulada Rhabdologiæ. Por este método, los productos se reducen a operaciones de suma y los cocientes a restas; al igual que con las tablas de logaritmos, inventadas por él mismo se tranforman las potencias en productos y las raíces en divisiones. El ábaco consta de un tablero con reborde en el que se colocarán las varillas neperianas para realizar las operaciones de multiplicación, división, extracción de la raíz cuadrada o cúbica. El tablero tiene su reborde izquierdo dividido en 9 casillas en las que se escriben los números 1 a 9.

Las varillas neperianas son tiras de madera, metal o cartón grueso. La cara anterior está dividida en 9 cuadrados, salvo el superior, divididos en dos mitades por un trazo diagonal. En la primera casilla de cada varilla se escribe el número, rellenando las siguientes con el duplo, triplo, cuádruplo y así sucesivamente hasta el nóncuplo del número al que corresponda la varilla.

Los dígitos resultados del producto se esciben uno a cada lado de la diagonal y en aquellos casos en los que sea inferior a 10, se escriben en la casilla inferior o derecha, escribiendo en la superior izquierda un cero o dejándola vacía.

Para poder realizar las operaciones generalmente se necesita más de un juego de varillas, ya que por lo común habrá cifras en las que los dígitos se repitan. Para disminuir el número de varillas necesarias, las originales de Napier constaban de 4 caras en las que se recogían los múltiplos de cuatro dígitos, de modo tal que las caras opuestas de la varilla sumaran 9 y estando los múltiplos correspondientes a los dígitos 5 a 9 invertidos como muestra la figura. Cada uno de los dígitos aparece en cuatro varillas diferentes, de modo que el juego completo de 10 varillas permite expresar números hasta de 10 cifras siempre y cuando un dígito no aparezca repetido más de 4 veces.

Multiplicación

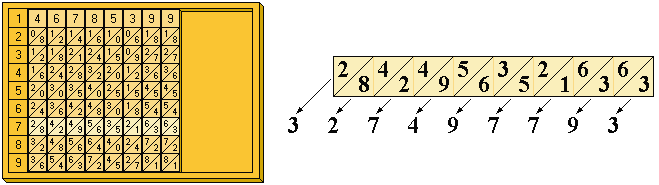
Provistos del conjunto descrito, supongamos que deseamos calcular el producto del número 46785399 por 7. En el tablero colocaremos las varillas corespondientes al número, tal como muestra la figura, haciendo posteriormente la lectura del resultado en la faja horizontal correspondiente al 7 del casillero del tablero, operación que sólo requiere sencillas sumas, con llevada naturalmente de los dígitos situados en diagonal.

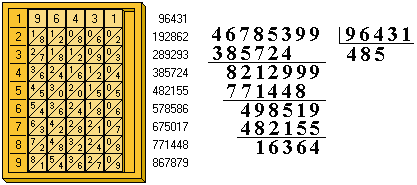
Comenzando por la derecha obtendremos las unidades (3), las decenas (6+3=9), las centenas (6+1=7), etc.Si algún dígito del número que deseamos multiplicar fuera cero, bastaría dejar un hueco entre las varillas.Supongamos que queremos multiplicar el número anterior por 96.431; operando análogamente al caso anterior obtendremos rápidamente los productos parciales del número por 9, 6, 4, 3 y 1, colocándolos correctamente y sumando, obtendremos el resultado total.

División

Igualmente podrían realizarse divisiones una vez conocidos los 9 productos parciales del dividendo; determinados éstos mediante el ábaco, basta seleccionar el inmediatamente inferior al resto sin necesidad de realizar los molestos tanteos que requieren las divisiones realizadas a mano.

Raíz cuadrada Como sabemos, para extraer una raíz cuadrada primeramente, debe agruparse los dígitos de dos en dos desde la coma, tanto hacia la derecha como la izquierda, quedando el número de la forma siguiente:

... xx xx xx xx , xx xx xx ...

Tomando el par (que podrá ser un sólo dígito) de la izquierda (xx), se obtiene la cifra a entera tal que su cuadrado sea igual o menor que el par. Esta será la primera cifra de la solución. Restando del par el cuadrado del entero así encontrado, obtenemos el resto:

ra = xx - a² (Si el primer par fuera 07, la cifra a sería 2, y el resto 7-4=3)

Posteriormente, y de forma iterativa, se añade al resto el siguiente par, quedando un número de la forma yxx (y, el resto anterior, xx el par añadido) que llamaremos Ra. La siguiente cifra de la solución deberá ser tal que el cuadrado de la solución parcial ab (siendo ab un número de dos dígitos, no un producto) sea menor que xxxx (los dos primeros pares del radicando):

(ab)² = (a·10 + b)² = (a·10)² + 2·a·10·b + b² < xxxx

despejando:

2·a·10·b + b² < xxxx - (a·10)² = R (2·a·10 + b)·b < Ra (I)

Operando de igual modo una vez conocidas las cifras ab, deberá determinarse la tercera cifra de la solución (c) y siguientes (d, e, ...) que, como fácilmente se puede demostrar operando análogamente al caso anterior, deberán cumplir:

(2·(ab)·10 + c)·c < Rb (II) (2·(abc)·10 + d)·d < Rc (III) (2·(abcd)·10 + e)·e < Rd (IV) ...

right‎

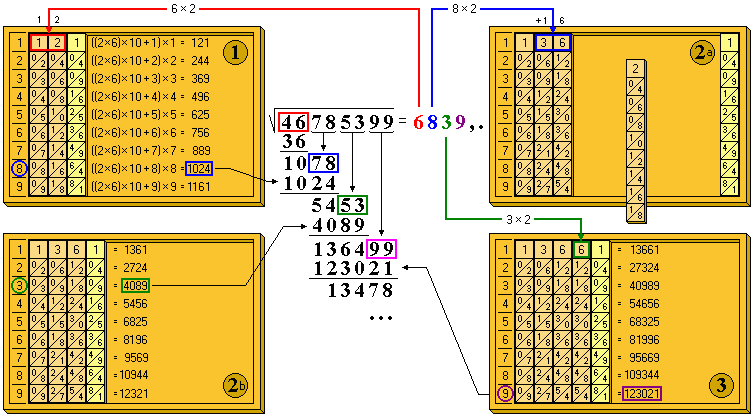
Los productos indicados pueden obtenerse fácilmente con el ábaco de Napier, pero para ello es necesaria una varilla auxiliar tal que en cada faja horizontal recoja los cuadrados de los números correspondientes; la varilla original de Napier para los cuadrados (pro quadrata) añadía una segunda columna con los duplos y una tercera con los números. Conocida la primera cifra a, colocamos en el ábaco la (o las) varillas correspondientes al duplo de a. Hecho esto, bastará añadir la varilla de los cuadrados para encontrar el número tal que se cumpla la ecuación (I), que será el correspondiente a la faja b. Dicho número deberá sustrarse de Ra para encontrar Rb. Encontrado b, retiramos la varilla auxiliar de los cuadrados y se coloca en el tablero la varilla correspondiente a 2·b; pueden darse dos casos, si b es menor que 5, el doble tendrá sólo una cifra con la que bstará colocar la varilla; en caso contrario (igual o mayor que 5) el duplo será mayor de 10, por lo que será necesario incrementar la última varilla colocada en una unidad. Ejemplo. Se desea obtener la raíz cuadrada del número 46 78 53 99. Se toma el primer par (46) y se determina el cuadrado inmediatamente inferior, que resulta ser 36 (49 que es el siguiente es mayor que 46), de modo que la primera cifra de la solución es 6, y el resto: 46 - 6·6 = 46 - 36 = 10. Se colocan las varillas de 6·2 = 12 en el tablero, y seguidamente la varilla auxiliar de los cuadrados. Componemos el resto y el siguiente par obteniendo el número 1078 que no deberá ser superado por el cuadrado de (6b). Leemos en el ábaco (1) el valor 1024, encontrando que b= 8 y el nuevo resto 1078 - 1024 = 54, descendiendo el siguiente par, obtenemos un valor de 5453. Se colocan las varillas correspondientes al doble de 8; por ser 16 (>10), se retira la última varilla, la del 2, sustituyéndola por la del 3 (es decir, se le suma una unidad) y se añade la varilla del 6. El ábaco queda como se muestra en (2a). Como puede observarse, las cifras colocadas son las correspondientes al doble de la solución encontrada hasta el momento (68·2 = 136); es decir, el 2abc.. de las ecuaciones anteriores.

Hecho esto, se vuelve a colocar la varilla auxiliar, y operando como en el caso anterior, obtenemos (2b) la tercera cifra: 3, siendo el resto 1364. Se desciende el siguiente par obteniendo un valor 136499, se coloca la varilla 6 (3·2) y encontramos el siguiente dígito 9 y el resto 13478. Mientras el resto sea distinto de cero se puede seguir obteniendo cifras significativas. Por ejemplo, para obtener el primer decimal, bajaríamos el par 00 obteniendo el número 1347800 y colocaríamos las varillas del 9·2 = 18, quedando en el tablero las siguientes: 1-3-6-7(6+1)-8-auxiliar. Haciendo la comprobación, se obtiene el primer decimal = 9.

Raíz cúbica

El procedimiento es similar al descrito para la extracción de raíces cuadradas, con la salvedad de que ahora, por la imposibilidad de incluir todos los términos en el cálculo será necesaria una comprobación adicional del resto. Comenzamos, como en el caso anterio, por agrupar las cifras del radicando en grupos de tres comenzando desde el punto decimal:

... xxx xxx xxx xxx , xxx xxx xxx ...

Tomando la terna (que podrá ser un sólo dígito) de la izquierda, se obtiene la cifra a entera tal que su cubo sea igual o menor que la terna. Esta será la primera cifra de la solución. Restando de la primera terna del radicando el cubo del entero así encontrado, obtenemos el resto, con la misma notación que en el caso anterior:

ra = xxx - a³ (Si la primera terna fuera 22, la cifra a sería 2, y el resto 22-8=14)

Posteriormente, y de forma iterativa, se añade al resto obtenido la terna siguiente, quedando un número de la forma yxxx (y, el resto anterior, xxx la terna añadida) que llamaremos Ra. La siguiente cifra de la solución deberá ser tal que el cubo de la solución parcial ab (siendo ab un número de dos dígitos, no un producto) sea menor que xxxxxx (las dos primeras ternas del radicando):

(ab)³ = (a×10 + b)³ = (a×10)³ + 3×(a×10)²×b + 3×(a×10)×b² + b³ < xxxxxx

despejando: 3×(a×10)²×b + 3×(a×10)×b² + b³ < xxxxxx - (a×10)² = R

agrupando: [3×a²×100×b + b³] + [(3×a×10)×b²] < Ra (I) Operando de igual modo una vez conocidas las cifras ab, deberá determinarse la tercera cifra de la solución (c) y siguientes (d, e, ...) que, como fácilmente se puede demostrar deberán cumplir ecuaciones análogas a la ecuación (I).

right‎

Los productos indicados pueden obtenerse fácilmente con el ábaco de Napier usando una varilla auxiliar (pro cubica) tal que en cada faja horizontal recoja los cubos de los números correspondientes, situando las centenas en la casilla superior y las decenas y unidades en la inferior. Además, se añaden dos columnas auxiliares con los cuadrados y los dígitos, tal como muestra la figura. Supongamos que deseamos obtener la raíz cúbica del número 22 022 635 627. Tomamos la primera terna (22) y determinamos el cubo inmediatamente inferior, que resulta ser 8 (27 que es el siguiente es mayor que 22), de modo que la primera cifra de la solución es a=2, y el resto: 22-8=14; descendiendo la segunda terna obtenemos Ra=14022. Para evaluar el primer sumando de la ecuación (I), colocamos las varillas correspondientes a 3×a² a la izquierda del tablero y a continuación la varilla de los cubos. En nuestro caso, por ser la primera cifra significativa obtenida un dos, tendremos que colocar las varillas del número 3×a² = 12. Con las varillas en dicha disposición, buscamos al igual que en el caso de la raíz cuadrada, el término menor que el resto, dándose éste en la novena fila, para la cual obtenemos 11529 < 14022. A este primer sumando de (I) hemos de sumarle el segundo. Para ello colocamos la varilla correspondiente a 3×a a la derecha de la varilla de cubos; en nuestro caso colocamos la varilla seis (3×2). Hecho esto el segundo sumando se obtendrá multiplicando por el cuadrado de la segunda cifra de la solución que llamábamos b. Probamos con b=9 (figura 2a), cuyo cuadrado es 81 y sumando al resultado anterior obtenemos 16389 > 14022, por tanto 9 no es la solución. (Nota: dado que en (I) el segundo sumando está multiplicado por 10, hemos de dejar un espacio a la derecha al realizar la suma; el resultado de 1×6 corresponde a las decen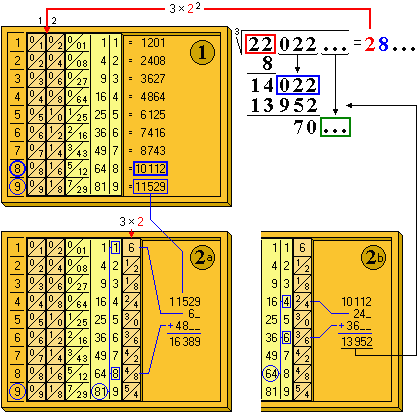as). Rechazado el nueve, probamos con b = 8. El primer sumando se obtiene, como antes, con las primeras varillas y la de los cubos, siendo el resultado 10112. Calculamos ahora el segundo sumando, siendo el cuadrado de b igual a 64 y sumando el resultado al anterior obtenemos un total de 13952, menor que 14022, por lo que la segunda cifra de la solución es b = 8. Para calcular la tercera cifra de la solución tenemos que sustituir en el tablero las varillas correspondientes a 3×a² por las correspondientes a 3×(ab)², siendo ab las dos cifras de la solución hasta ahora obtenidas. A pesar de que con el ábaco podríamos realizar la operación en dos pasos, Napier propone un método simplificado para hacerlo, partiendo de las cifras de la solución previamente calculadas; desarrollamos el término a calcular (ab es el número de dos cifras):

3×(ab)² = 3×(a×10 + b)² = = 3×(a×10)² + 3×b² + 3×2×(a×10)×b = 3×(a×10)² + 3×b² + a×b×10 + 5×(a×10)×b

La descomposición del término 6×a×b en a×b+5×a×b puede parecer trivial pero simplifica los cálculos:

• El primer sumando ya figura en el ábaco y se corresponde con las dos primeras varillas colocadas; en nuestro caso 1200, ahor ahay que añadir dos ceros porque una vez obtenido b, a pasa a ser decenas.
• El segundo término es el triple del cuadrado de la última cifra de la solución encontrada (8); buscando el cuadrado en la varilla obtenemos 64 y multiplicándolo por tres 192 (se puede usar la varilla tres pues los cuadrados ya están en la varilla auxiliar).
• El tercer término se obtiene multiplicando la solución anterior por la nueva cifra, en este caso 2×8 = 16 y por diez, quedando 160.
• El último término es cinco veces el anterior, bastando dividirlo por dos (80) y multiplicarlo por 10: 800.

Sumando, obtenemos 3×(ab)² = 1200 + 192 + 160 + 800 = 2352; varillas que colocaremos a la izquierda del tablero en sustitución de las varillas 1 y 2 para proceder al cálculo de la tercera cifra. Igualmente tendremos que actualizar las varillas de la derecha con el triple de la cifra encontrada; en el ejemplo 3×8 = 24; por tanto sustituimos la varilla 6 por la 8 y añadimos la varilla 4. En la figura siguiente se muestran los pasos para la obtención de las dos cifras siguientes. Para la tercera cifra, observamos (figura 3) que el producto menor es 235201, mayor que el resto 70635, luego la tercera cifra es c=0. En este caso bastará añadir dos varillas cero a la izquierda y una a la derecha para buscar la cuarta cifra. Buscando en el ábaco (figura 4) el producto inmediatamente inferior al resto 70635627 corresponde a la fila 3 (70560027), sumándole a ésta el producto de las varillas de la derecha por el cuadrado de 3 (9) obtenemos 70635627, quedando un resto nulo, por lo que la raíz cúbica es exacta; la raíz buscada es 2803.

Se supone que la raíz no hubiera sido exacta y deseáramos encontrar el primer decimal; para ello deberíamos sustituir las varillas 235200 por las correspondientes a 3×2803; siguiendo el procedimiento descrito con anterioridad, necesitaríamos calcular primero el triple del cuadrado del último dígito obtenido 3×3²=27, y luego el producto de la última cifra por las restantes y por diez; es decir 3×280×10=8400 y dividir el resultado por la mitad y multiplicarlo por 10 (42000); resulta obvio que cuantas más cifras significativas se haya calculado, mayor será la dificultad en obtener este producto, a no ser claro está que coloquemos las varillas apropiadas en el ábaco. Si realiza la operación, las varillas a colocar serían:

23520000 + 27 + 8400 + 42000 = 23570427

Como alternativa, y considerando que para la obtención de otra cifra significativa tenemos que actualizar las varillas a izquierda y derecha introduciendo el último dígito calculado, podemos hacer lo siguiente. Obtenida la última cifra 3; leemos su producto en las varillas de la derecha, 2520 y lo multiplicamos por 10 obteniendo 25200. Actualizamos dichas varillas con el triple del último dígito, es decir colocamos la varilla del nueve y volvemos a calcular el producto por el último dígito calculado obteniendo 25227. Añadiendo ambas cifras a la original:

23520000 + 25200 + 25227 = 23570427

Es decir el mismo resultado anterior, pero leído directamente del ábaco y quedando éste preparado para obtener la siguiente cifra significativa. Curiosamente Napier no recoge este método en su descripción del ábaco., siendo más sencillo que el propuesto por él.

Modificaciones

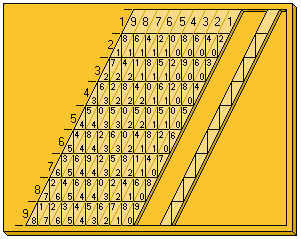
Durante el siglo XIX, el ábaco neperiano sufrió una transformación para facilitar la lectura. Las varillas comenzaron a fabricarse con una inclinación del orden de 65º, de modo que los triángulos que debían sumarse quedaran alineados verticalmente. En este caso, en cada casilla de la varilla se consigna la unidad a la derecha y la decena (o el cero) a la izquierda. Las varillas estaban fabricadas de modo tal que el grabado vertical y horizontal era más visible que las juntas entre las varillas, facilitándose mucho la lectura al quedar el par de componentes de cada dígito del resultado en un rectángulo. Así, en la figura se aprecia inmediatamente que:

987654321 x 5 = 4938271605

Ábaco de fichas

Además del ábaco anterior, Napier construyó un ábaco de fichas. Ambos, reunidos en un único aparato consituyen una joya histórica, única en Europa que posee el Museo Arqueológico Nacional de España. El aparato es una magnífica caja de madera con embutidos de hueso. En la parte superior contiene el ábaco rabdológico, mientras que en la inferior se encuentra el segundo ábaco que consta de 300 fichas de almacenadas en 30 cajones de las que 100 están cubiertas de cifras y doscientas muestran pequeños taladros triangulares que permiten ver únicamente ciertas cifras de las fichas de números cuando se superponen a aquéllas, de forma tal que merced a la hábil colocación de unos y otros pueden realizarse multiplicaciones hasta el asombroso límite dede un número de 100 cifras por otro de 200. En las portezuelas de la caja se encuentran además las primeras potencias de los números dígitos, los coeficientes de los términos de las primeras potencias del binomio y los datos numéricos de los poliedros regulares. Se desconoce quién fue el autor de esta riquísima joya, ni si es de autoría española o vino del extranjero, aunque es probable que originalmente perteneciera a la Academia de Matemáticas creada por Felipe II o que la trajese como regalo el Príncipe de Gales. Lo único que puede asegurarse es que se conservaba en Palacio, de donde pasó a la Biblioteca Nacional y posteriormente al Museo Arqueológico Nacional, donde aún se conserva. En 1876, el gobierno español envió el aparato a la exposición de instrumentos científicos celebrada en Kensington, donde llamó extraordinariamente la atención, hasta el punto de que varias sociedades consultaron a la representación española acerca del origen y uso del aparato, lo que motivó que D. Felipe Picatoste escribiera una monografía que fue posteriormente enviada a todas las naciones, sorprendiendo el hecho de que el ábaco sólo fuera conocido en Inglaterra, país de origen de su inventor.

Fuente

• Diccionario Enciclopédico Hispano-Americano, Montaner y Simón Editores, Barcelona, 1887, Tomo I, pp. 19-20.
• Napier, John [1617]. Andreas Hart: Rabdologiæ, seu numerationis per virgulas, 1ª edición (latín), Edimburgo.