Congruencia (geometría)
| ||||||
Congruencia (geometría):En matemáticas, dos figuras de puntos son congruentes si tienen los lados iguales y el mismo tamaño (o también, están relacionados por un movimiento) si existe una isometría que los relaciona: una transformación que es combinación de translaciones, rotaciones y reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.
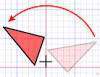
Si se puede convertir una forma en otra usando giros, volteos y deslizamientos, las dos formas son congruentes:
Después de estas transformaciones (girar, voltear, deslizar) la forma sigue teniendo el mismo tamaño,área, ángulos y longitudes de líneas.
Sumario
Ángulos congruentes
Se denomina ángulos congruentes a aquellos ángulos que tienen la misma medida. Los ángulos opuestos por el vértice son un ejemplo de ángulos congruentes. Las diagonales de un paralelogramo configuran ángulos opuestos por el vértice congruentes.
Congruencia de triángulos
Observa los siguientes triángulos:
Al mirar los dos pares de triángulos se puede apreciar que en ambos los triágulos tienen entre si la misma forma y tamaño.
Cuando se cumplen estas dos condiciones se dice que los triángulos son congruentes; esta palabra (congruente) se simboliza o representa con el símbolo.
La congruencia de triángulos estudia los casos en que dos o más triángulos presentan ángulos y lados de igual medida o congruentes.
Dos triángulos son congruentes si sus lados correspondientes tienen la misma longitud y sus ángulos correspondientes tienen la misma medida.
Si el triángulo ABC es congruente al triángulo DEF, la relación puede ser escrita matemáticamente así:
Definición
Se dice que un Δ ABC es congruente con otro Δ DEF si sus lados respectivos son iguales y sus ángulos respectivos también lo son.
Al observar los triángulos de la figura puede apreciarse que tienen lados respectivamente congruentes, que son:
También tienen ángulos respectivamente congruentes:
Criterios de congruencia
En muchos casos es suficiente establecer la igualdad entre tres partes correspondientes y usar uno de los criterios para deducir la congruencia de dos triángulos. Los criterios de congruencia corresponden a los postulados y teoremas que enuncian cuáles son las condiciones mínimas que deben reunir dos o más triángulos para que sean congruentes. Estas son: 1.- Congruencia de sus lados 2.- Congruencia de sus ángulos Para que dos triángulos sean congruentes, es suficiente que sólo algunos lados y/o ángulos sean iguales.
Postulados o criterios básicos de congruencia de triángulos
Postulado LAL
LAL significa lado-ángulo-lado. Dos triángulos son congruentes si tienen dos lados y el ángulo determinado por ellos respectivamente iguales.
Postulado ALA
ALA significa ángulo-lado-ángulo. Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos, respectivamente, iguales.
Postulado LLA
LLA significa lado-lado-ángulo Dos triángulos son congruentes si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.
Postulado LLL
LLL significa lado-lado-lado. Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.