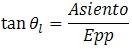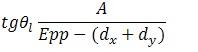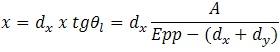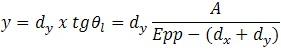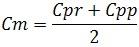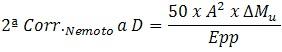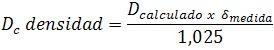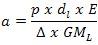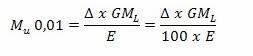Desplazamiento (náutica)
| ||||||
Desplazamiento (náutica). Es el peso de la embarcación y el peso del volumen de agua desplazada por el casco, incluyendo todos los apéndices sumergidos. De acuerdo con el principio de Arquímides, se puede decir que, desplazamiento, en general, es el peso del volumen del líquido desalojado por el buque en una determinada flotación.
Sumario
Cálculo del desplazamiento
El cálculo del desplazamiento máximo se hace con la embarcación lista para salir a navegar, con todo su equipo e instalaciones fijas, con los motores de mayor peso para los que esté diseñada, con los tanques de combustible y agua potable llenos, y el número máximo de personas autorizadas, (75 Kgs por persona), elementos de seguridad, contra incendios, salvamento y navegación.
Según la carga, el desplazamiento puede ser, además del máximo:
a) Desplazamiento en rosca:
b) Desplazamiento en lastre:
c) Desplazamiento en carga:
El 'Porte es la diferencia entre el Desplazamiento en lastre y el desplazamiento en máxima carga.
El Peso Muerto (PM) es la diferencia entre el desplazamiento en máxima carga y el desplazamiento en rosca, es decir, el peso máximo que el buque puede cargar.
Desplazamiento del Buque
El desplazamiento se define como; Δ =vsumergido· γmar, y representa el peso del agua desplazada por este volumen (Principio de Arquímedes). Las unidad utilizada es toneladas y, en el sistema anglosajón, toneladas largas (en inglés, long tons). Desde el punto de vista de la teoría del buque se distinguen:
Desplazamiento en rosca, Δr (en inglés, lightweight displacement): es el peso del buque tal como lo entrega el astillero; esto es, sin combustible, pertrechos, víveres ni tripulantes.
Desplazamiento en estándar, Desplazamiento Liviano, Δe Es el peso del buque completo, además de equipos (botes, instrumentos de navegación, etc.) más tripulación con su equipaje, líquidos en circulación, víveres, munición (en los buques de guerra), agua dulce y aceite lubricante. Quedarían excluidas el combustible y el agua de reserva para las calderas.
Desplazamiento en lastre, Δl: es el peso del buque en rosca más todo lo necesario para que pueda navegar (combustible, agua potable, provisiones y pertrechos), pero sin carga.
Desplazamiento máximo, Δm: es el peso que alcanza cuando está sumergido hasta la línea de máxima carga (agua de mar en verano de la marca de Plimsoll). El dato de «desplazamiento» de un buque, si no se especifica otra cosa, se refiere al desplazamiento máximo.
La diferencia entre el desplazamiento máximo y el desplazamiento en rosca se denomina «tonelaje de porte bruto» o «tonelaje de peso muerto», TPM (en inglés, deadweight tonnage). Así, el tonelaje de peso muerto incluye el peso de la carga, incluyendo pasajeros y tripulación, y el de los consumibles (combustible, víveres, agua potable...) mencionado más arriba.
La diferencia entre el desplazamiento máximo y el desplazamiento en lastre se conoce como «capacidad de carga», que indica el peso de la carga que es posible transportar en ese buque. No es utilizado habitualmente por los navieros y agentes de transporte marítimo.
Cálculo del desplazamiento con las curvas hidrostáticas
Curvas hidrostáticas, son las curvas que reflejan del comportamiento de la carena de un buque para los diferentes calados (estados de carga). Reciben el nombre de carena derecha pues son calculadas para la condición de adrizamiento. Las confecciona el astillero y las entrega al capitán para su aplicación en el cálculo de la estabilidad transversal inicial de un buque. Sin duda y a este fin la curva más significativa es la que determina la altura del metacentro transversal (curva Figura 1). Otras curvas son empleadas en los cálculos de calados finales y de asiento. Las curvas de parámetros verticales están referidas a la línea base o canto superior de la quilla. Las curvas de parámetros longitudinales, (posición longitudinal del centro de carena, etc) están referidas o bien a la sección maestra ó a la perpendicular de popa.
Calculo del desplazamiento del buque
El cálculo del desplazamiento del buque, está basado en el valor del calado medio para la línea de flotación paralela a la quilla, esto ocurre cuando el buque esta en aguas iguales y los calados se leen en las perpendiculares respectivas.
La perpendicular de popa es la línea vertical que pasa por el eje de la mecha del timón, si es colgado o por la cara de popa del codaste popel. La eslora entre perpendiculares es la distancia horizontal entre ambas líneas medida paralelamente a la quilla. Ahora bien ese desplazamiento está sujeto a una serie de correcciones:
Corrección por escora
Se hace la media entre los calados leídos en cada extremo. Si se lee solo el calado en una de la bandas a proa y a popa y en las dos bandas al centro calculamos el valor de la escora :
Y con este valor corregimos los calados de las cabezas calculadas ( es necesario conocer del plano de formas la manga en la zona donde se ha leído el calado). Con estas operaciones ya tenemos aplicada la primera corrección Las marcas de los calados muchas veces no coinciden en las perpendiculares respectivas (proa, popa) por ello al proceder a su lectura en la escala marcada hay una diferencia con la que correspondería a la escala en perpendiculares, este fenómeno aparece cuando el buque esta en lastre, para su corrección se tiene que proceder de la siguiente forma: Calculamos la inclinación longitudinal
Cada buque tiene un plano en el que se puede calcular la distancia para cada calado entre la perpendicular correspondiente y la escala de calados marcada en el buque. Conocida la distancia para el calado calculado la corrección a aplicar depende del asiento y de la posición de la escala con respecto a las perpendiculares, ya que esta puede estar a proa o a popa (normalmente en proa la escala de calados está a popa de la perpendicular y en popa a proa.) En muchos buques, las formas de la roda y del codaste, no permite el trazado de estas líneas, por lo que las escalas de calados tienen que ir marcadas en las zonas posibles, fuera de las perpendiculares, en estos casos, una vez que leemos las marcas, a los valores obtenida, hay que aplicarles una corrección, cuyo valor depende del asiento del buque Cpr= Calado leido a proa Cpp= Caldo leido a popa x = corrección al calado de proa y = Corrección al calado de popa dx= Distancia de escala de calados a pp. proa dy= Distancia de escala de calados a pp. de popa Asiento A = Cpp- Cpr ( + Apopante, - Aproante) Epp = Eslora entre perpendiculares. Calculamos la inclinación longitudinal:
Los valores de las correciones a los calados leidos son: 1.-para el calado de proa
2.- Para el calado de popa
Corrección al desplazamiento por densidad
El desplazamiento del buque es igual al peso del agua ocupada por su carena, y su valor es el volumen de carena multiplicado por el peso específico del agua en la que flota el buque. El peso específico del agua dulce a 4º Centígrados es 1, por lo que un litro de agua a esa temperatura pesa 1 kg. 4ºC es la temperatura a la cual la densidad del agua dulce es la mayor. Las curvas hidrostáticas del buque, permiten calcular su desplazamiento, para cualquier calado, con el buque en aguas iguales y para una densidad del agua igual a 1,025 tn. por m3. que es la densidad media del Atlántico norte. El valor de la densidad, varía con la salinidad y la temperatura. Si tomamos agua dulce a 4º C, su peso específico es 1 pero a 15ºC es de 0,99913, por lo que un metro cúbico de agua dulce a 4ºC pesa 1.000 kg. pero a 15ºC su peso es de 999,13 kg. Pasos a seguir Lectura de los calados proa, popa, centro babor y estribor Determinación de la densidad del agua donde flota el buque Cálculo de la temperatura del agua de mar. -Calculamos la corrección:
d = distancia entre perpendicular y escala de calados Signos: En calado de proa corrección: + si asiento positivo (escala a proa de perpendicular) + si asiento negativo (escala a popa de perpendicular) - si asiento negativo (escala a proa de perpendicular) - si asiento positivo (escala a popa de perpendicular) En el calado de popa las correcciones tienen los mismos signos anteriores. Aplicamos las correcciones calculadas a los calados corregidos de escora y tendremos los calados en perpendiculares. En algunos casos la inclinación longitudinal se calcula en vez de con la eslora entre perpendiculares con la distancia entre marcas de calados, ya que el asiento calculado corresponde a la posición de las escalas, si así lo hacemos, la distancia entre marcas es:
d1 distancia en proa, y d2 distancia en popa de escalas respectivas a las perpendiculares. Con estos datos calculamos
Con el calado leído en el medio, si tenemos diferencia con el anterior es por que el buque tiene quebranto arrufo Si calado leído en el medio > calado medio arrufo Si calado leído en el medio < calado medio quebranto. Esta situación origina una diferencia en el valor del volumen sumergido calculado en las curvas hidrostáticas, que se construyen para el buque con flotaciones planas.
Corrección al desplazamiento por asiento o corrección NEMOTO.
Al calcular el desplazamiento corregido se obtiene un valor, pero el Ingeniero Nemoto, encontró que si se utilizan las curvas de Bonjean para determinar el desplazamiento del buque, siempre que había un asiento aparecía una diferencia, siendo el desplazamiento calculado por las curvas de Bonjean mayor que el obtenido en las hidrostáticas con el calado medio. La razón de esta diferencia viene dada por las formas irregulares del buque en los finos de proa y popa. Aplicando una serie de ecuaciones según el método de Taylor's, e integrando en función de la eslora del buque encontró la diferencia del desplazamiento, que se obtiene mediante la aplicación de la siguiente fórmula que lleva su nombre:
A = Asiento en metros ΔMu Diferencia entre los valores del Momento unitario de asiento calculado en curvas con Cm+0,5 y Cm-0,5 El valor de esta corrección viene en toneladas y siempre es positiva.
Corrección por densidad
Las curvas hidrostáticas del buque, nos dan el valor del desplazamiento con el calado medio cuando el buque flota en agua dulce de densidad 1 y en agua salada de densidad 1,025 Tn/m3 Cuando el valor de la densidad no coincide con uno de los valores indicados, para calcular el valor real del desplazamiento, tomamos muestras de agua de mar y medimos el valor de su densidad. Calculado este valor el desplazamiento corregido por densidad es:
Cálculo del Momento Unitario Hemos definido el momento de asiento unitario como el momento escorante longitudinal que es necesario aplicar al barco, medido en toneladas x metro, para producir una alteración de 1 cm. Como ya he comentado anteriormente, es intuitivamente evidente que esta magnitud dependerá del desplazamiento del barco (equivalentemente, de su calado medio). Se obtendrá, por tanto, de las curvas hidrostáticas del barco para cada estado de carga. Ahora bien, podemos deducir fácilmente una expresión útil para Mu en términos de la altura metacéntrica longitudinal GML que introdujimos al estudiar la estabilidad estática longitudinal. No es sorprendente que pueda relacionarse Mu con GML puesto que, como indica la ecuación tgθL.p = GG'/GML, GML determina la escora longitudinal producida y, a su vez, la escora longitudinal es quien provoca la alteración. Así, hemos visto anteriormente que la alteración a y la escora longitudinal θL están relacionadas mediante la ecuación tgθL = a/E, donde E es la eslora entre perpendiculares. Por tanto, combinando estas ecuaciones encontramos el resultado siguiente:
en la que hemos hecho uso, además, del valor GG' = p x dl/ Δ para el desplazamiento provocado en el centro de gravedad al trasladar el peso p longitudinalmente una distancia dl. Ese traslado ha producido un par escorante cuyo momento es, evidentemente, p x dl así que la ecuación anterior nos está diciendo que el momento escorante necesario para producir una alteración a es Mesc = a x Δ x GMI/E. Puesto que el momento de asiento unitario Mu se define como el momento necesario para producir una alteración a 1 cm, estará dado por el valor del Mesc que en la ecuación anterior produce una a = 1 cm = 0.01 metros. Es decir,
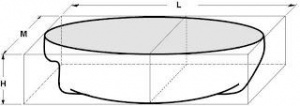
ecuación en la que GML y E se medirán en metros, Δ en toneladas y el resultado para Mu estará en toneladas x metro. Esta ecuación nos permitirá obtener la altura metacéntrica longitudinal GML a partir del valor de Mu obtenido de las curvas hidrostáticas entrando con el desplazamiento Δ que tenga el barco en las circunstancias en las que se encuentre. Coeficientes de forma Coeficiente de total, de bloque ó de block (Cb) es la relación entre el volumen de la carena de un casco y el paralelepípedo que lo contiene (L=Eslora, M=Manga y H=Calado). (Figura superior). Cb = Vol. de carena / Vol. del paralelepípedo = Vc / (L x M x H)
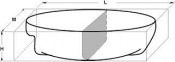
Coeficiente de flotación Se define como coeficiente de flotación (Cf) a la relación entre el área del plano de flotación (figura superior en celeste) y el área del rectángulo que la circunscribe. Cf = Área de flotación / Área del rectángulo = Af / (L x M) Coeficiente prismático o longitudinal Se define como coeficiente prismático Cp a la relación entre el volumen de la carena y el volumen de un cilindro cuya base tiene igual área que la sección maestra. Cp = Volumen de carena / Volumen cilindro = Vc / (Am x L)
Coeficiente de sección maestra Se define como coeficiente de sección maestra Cm a la relación entra el área de la sección maestra y el rectángulo que la circunscribe. Cm = Área de sección maestra / Área rectángulo = Am / (M x H) Toneladas por centímetro de inmersión Se denomina toneladas por centímetro de inmersión ó TPC a la masa en toneladas que debe agregarse a una embarcación, aplicado éste en el centro de gravedad de un buque, para lograr un incremento de un centímetro en el calado medio. El nuevo plano de flotación se mantiene paralelo al inicial. Dado que la carena de un buque no es un paralelogramo, el valor del coeficiente TPC varía en función del calado medio considerado. Esta variación de calado es igual al peso de la rebanada de carena cuya base es el área de flotación, Af inicial y su altura de un centímetro (volumen de la rebanada) por el peso específico del agua en que se encuentra flotando la embarcación. Para el caso de agua de mar con un peso específico de 1,025 t/m3 tendríamos
donde Af es el área de flotación. Las unidades se muestran en rojo. El coeficiente TPC es proporcional al área de flotación, por lo que a mayor tamaño de buque mayor será el valor TPC. Es muy usual encontrase para buques construidos en países sajones con el concepto toneladas por pulgada, el concepto es el mismo, pero debe tenerse en cuenta que se refiere a toneladas inglesas y no a toneladas métricas. Una tonelada inglesa o tonelada corta equivale a 907,18474 kg. Conocer este valor permite calcular con relativa facilidad la cantidad de carga a alijar para zafar una varadura que requiera una disminución de calado en una cantidad determinada de centímetros.
Tabla que relaciona Potencia de Motor con Desplazamiento
| Desplazamiento del barco en Toneladas. |
Potencia necesaria en CV-HP |
| 2 |
9 |
| 3 |
12,2 |
| 4 |
15,5 |
| 5 |
18,8 |
| 6 |
22,5 |
| 7 |
25,8 |
| 8 |
29 |
| 9 |
32,3 |
| 10 |
35,6 |
| 11 |
39,8 |
| 12 |
44,1 |
| 13 |
47,3 |
Estos valores de potencia de motor se tienen que tomar como la potencia necesaria en el eje, por lo que un incremento de un 10-15% sería admisible como consideración de la potencia al freno del motor, que es la que nos proporcionará el fabricante. Los resultados de nuestra hoja de cálculo junto con la recopilación de documentación que hemos realizado para desarrollar este artículo, nos llevan a pensar que podemos aplicar con bastante fiabilidad una regla general muy extendida y fácil de calcular, con la cual determinar a bote pronto y sin demasiadas complicaciones, cual es la potencia necesaria para la mayoría de los veleros de serie. LA REGLA FÁCIL Consiste en multiplicar por 4 CV las toneladas de desplazamiento del velero para el que deseamos saber la potencia necesaria. Este valor nos dará una potencia de motor aproximada que nos permitirá navegar a un 75% de la máxima potencia del motor, y así obtener una velocidad de crucero acorde a las expectativas de nuestra línea de flotación. Obviamente esta regla tiene que tomarse de acuerdo con un tipo de velero bastante estándar, con una forma de carena y una obra muerta convencionales. Para cualquier barco de características fuera de lo común será necesario evaluar alguna variación.
Fuentes
- ecured.cu Consultado: 11 de diciembre del 2013.
- surcando.com Consultado: 11 de diciembre del 2013.
- espanol.answers.yahoo.com Consultado: 11 de diciembre del 2013.
- fotosimagenes.org Consultado: 11 de diciembre del 2013.
- masmar.com Consultado: 11 de diciembre del 2013.
- cntfacs.com.ar Consultado: 11 de diciembre del 2013.
- barcosnautica.com Consultado: 11 de diciembre del 2013.
- wikipedia.org Consultado: 11 de diciembre del 2013.