Rombo
| ||||||
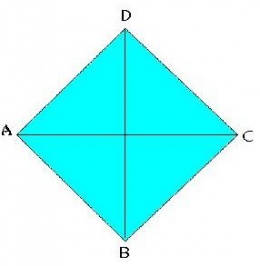
En la geometría euclidiana plana, el rombo es un paralelogramo, cuyos cuatro lados tienen igual longitud.
Las diagonales de un rombo cuentan con propiedades usadas en la fabricación de periscopios, para ello se utilizan rombos cuyos ángulos son rectos.
Un rombo que tiene un ángulo recto se denomina cuadrado [1].
Sumario
Área
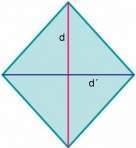
Siendo d y d’ las diagonales del rombo, el área se calcula con la siguiente fórmula:
- Alternativamente
Sean d1 y d2 las dos diagonales de un rombo, entonces el área, se denota con A = d1×d2÷2
Si conociéramos el área de uno de los cuatro triángulos iguales en que queda dividido un rombo por las diagonales, entonces, siendo AT, el área de uno de esos triángulos, puede calcularse el área del rombo como:
- A = 4 * AT
Mayor área
Un rombo de lado constante alcanza su área máxima cuando sus diagonales son iguales; en el caso de que el rombo sea un cuadrado.[2]
- Se tiene (d/2)2 + (d´/2)2 = l2 , de donde d2 + d'2 = 4 l2.
- También A = d×d'/2, de aquí 4A2 = d2×d'2, como la suma de los cuadrados de las diagonales es constante, el producto 4A2 alcanza su valor máximo cuando los factores son iguales. Y tomando la raiz cuadrada, resulta que A = d×d'/2 alcanza el valor máximo si d = d'.
Perímetro
El Perímetro (p) del Rombo se calcula como la suma de las longitudes de sus 4 lados. Siendo l la longitud de uno de sus lados, y teniendo en cuenta que son iguales los cuatro, podemos reducir la fórmula como sigue:
p = 4 * l.
Diagonales
Las diagonales del Rombo, al igual que las de cualquier paralelogramo, se cortan en su punto medio, además entre ellas forman un ángulo de 900.
Nota: Si el lado del Rombo es l, sus diagonales d y d’, y sabiendo que se cortan en su punto medio por ser paralelogramo, se cumple, por tanto, la siguiente relación referida al Teorema de Pitágoras:
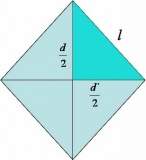
(d/2)2 + (d´/2)2 = l2
Es decir, que la suma de los cuadrados de las longitudes de dos semidiagonales, es igual al cuadrado de la longitud del lado del Rombo (Ver imagen)
Propiedades
- Los cuatro lados son iguales.
- Los pares de ángulos opuestos son iguales.
- Cada dos ángulos contiguos son suplementarios (suman 1800).
- Sus dos diagonales se cortan en sus puntos medios.
- Sus dos diagonales son perpendiculares (forman un ángulo de 900).
- Cada diagonal es bisectriz de los ángulos cuyo vértices une (los divide en partes iguales).
Ver también
Fuentes
- Miyares Arturo y Escalona Jose M. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974.