Diferencia entre revisiones de «Trapecio»
(Página creada con '{{Definición|Nombre=Cuadrilátero|imagen=Cuadrilátero.JPG|concepto=Polígono de cuatro lados}}'''Trapecio (Figura). '''Cuadrilátero que tiene dos lados …') |
|||
| Línea 1: | Línea 1: | ||
| − | {{Definición|Nombre=Cuadrilátero|imagen= | + | {{Definición|Nombre=Cuadrilátero|imagen=Trapecio_plantilla.JPG|concepto=[[Cuadrilátero]] con un solo par de lados paralelos.}}'''Trapecio (Figura). '''[[Cuadrilátero|Cuadrilátero]] que tiene dos lados paralelos y los otros dos no paralelos. Los lados paralelos reciben en general el nombre de [[Bases|bases]], denominándose base mayor al de mayor longitud, y base menor al otro. Se denomina altura del trapecio a la longitud de un [[Segmento|segmento]] de perpendicular comprendido entre ambas bases. |
== Área<br> == | == Área<br> == | ||
| − | Al igual que los demás cuadriláteros, el trapecio posee área. Esta puede calcular por las siguientes variantes: | + | [[Image:Trapecio_area.JPG|thumb|right|188x110px|Cálculo de área del Trapecio]]Al igual que los demás cuadriláteros, el trapecio posee área. Esta puede calcular por las siguientes variantes: |
| − | *Si se conoce la longitud de sus bases a y c, y de la altura (h), el área se calcula como la semisuma de las bases por la altura, o sea: | + | *Si se conoce la longitud de sus bases a y c, y de la altura (h), el área se calcula como la semisuma de las bases por la altura, o sea: [[Image:Trapecio_fórmula_area.JPG]]. Ver figura . |
| − | *Si se conoce la longitud de la paralela media (m) y de la altura (h), el área se calcula como: A = m * h.<br> | + | *Si se conoce la longitud de la paralela media (m) y de la altura (h), el área se calcula como: A = m * h. Ver figura.<br> |
| − | == Paralela media<br> == | + | == Paralela media<br> == |
| − | La paralela media es el segmento que une los dos puntos medios de los lados no paralelos del trapecio. En la figura anterior podemos ver d y b como puntos medios de los lados AD y BC respectivamente, y entonces m es la paralela media. Se calcula como la semisuma de las bases, o sea, m = (a + c) /2.<br> | + | La paralela media es el segmento que une los dos puntos medios de los lados no paralelos del trapecio. En la figura anterior podemos ver d y b como puntos medios de los lados AD y BC respectivamente, y entonces m es la paralela media. Se calcula como la semisuma de las bases, o sea, m = (a + c) /2.<br> |
== Perímetro == | == Perímetro == | ||
| Línea 53: | Línea 53: | ||
== Propiedades == | == Propiedades == | ||
| − | *La suma de los cuatro ángulos interiores equivale a cuatro rectos. | + | *La suma de los cuatro ángulos interiores equivale a cuatro rectos. |
| − | *Tiene dos diagonales en total, y desde un vértice se puede trazar solo una. | + | *Tiene dos diagonales en total, y desde un vértice se puede trazar solo una. |
*Las diagonales se cortan en un punto interior del trapecio. | *Las diagonales se cortan en un punto interior del trapecio. | ||
== Véase también == | == Véase también == | ||
| − | <span | + | <span style="display: none;" id="1284065516656S"> </span> |
| − | <span | + | <span style="display: none;" id="1284065514925S"> </span> |
*[[Triángulo|Triángulo]] | *[[Triángulo|Triángulo]] | ||
| Línea 69: | Línea 69: | ||
*[[Circunferencia|Circunferencia]] | *[[Circunferencia|Circunferencia]] | ||
*[[Círculo|Círculo]] | *[[Círculo|Círculo]] | ||
| − | *[[Cuadrilátero|Cuadrilátero]]<span | + | *[[Cuadrilátero|Cuadrilátero]]<span style="display: none;" id="1284065514966E">T </span> |
== Fuentes == | == Fuentes == | ||
| Línea 75: | Línea 75: | ||
*[[Encarta|Microsoft ® Encarta]] ® [[2007|2007]]. © [[1993|1993]]--[[2006|2006 ]]Microsoft Corporation. Reservados todos los derechos. | *[[Encarta|Microsoft ® Encarta]] ® [[2007|2007]]. © [[1993|1993]]--[[2006|2006 ]]Microsoft Corporation. Reservados todos los derechos. | ||
*[[Arturo Miyares|Miyares Arturo]] y Jose M Escalona. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. [[La Habana]]. [[Cuba]]. [[1974|1974]]. | *[[Arturo Miyares|Miyares Arturo]] y Jose M Escalona. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. [[La Habana]]. [[Cuba]]. [[1974|1974]]. | ||
| + | |||
| + | <br> | ||
<br> | <br> | ||
Revisión del 09:30 21 sep 2010
| ||||||
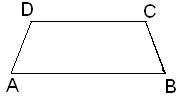
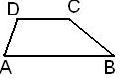
Trapecio (Figura). Cuadrilátero que tiene dos lados paralelos y los otros dos no paralelos. Los lados paralelos reciben en general el nombre de bases, denominándose base mayor al de mayor longitud, y base menor al otro. Se denomina altura del trapecio a la longitud de un segmento de perpendicular comprendido entre ambas bases.
Sumario
Área
Al igual que los demás cuadriláteros, el trapecio posee área. Esta puede calcular por las siguientes variantes:
- Si se conoce la longitud de sus bases a y c, y de la altura (h), el área se calcula como la semisuma de las bases por la altura, o sea:
. Ver figura .
- Si se conoce la longitud de la paralela media (m) y de la altura (h), el área se calcula como: A = m * h. Ver figura.
Paralela media
La paralela media es el segmento que une los dos puntos medios de los lados no paralelos del trapecio. En la figura anterior podemos ver d y b como puntos medios de los lados AD y BC respectivamente, y entonces m es la paralela media. Se calcula como la semisuma de las bases, o sea, m = (a + c) /2.
Perímetro
El Perímetro (p) del trapecio se calcula como la suma de las longitudes de sus 4 lados, es decir, con la fórmula A = a + b + c + d, siendo a, b, c, d, las longitudes de los cuatro lados del trapecio.
Clasificación
Los cuadriláteros de forma general se clasifican en dos grandes grupos:
- Cóncavos: Son aquellos cuadriláteros, que al menos uno de sus lados cumple la condición de que la línea que lo contiene, divide a la figura en dos partes, o sea, la deja en ambos semiplanos en que divide la línea al plano.
- Convexos: Son aquellos cuadriláteros que cumplen la condición de que al prolongar cualquiera de sus lados, la línea que lo contiene deja al cuadrilátero en un solo semiplano.
Tipos
Los cuadriláteros cóncavos no son de relevancia para el estudio en la escuela. Por esa razón en este artículo se hablará de los cuadriláteros convexos. Estos se dividen en Paralelogramos, Trapecios y Trapezoides.
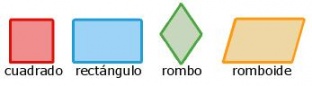
Paralelogramos: Tienen sus dos pares de lados opuestos paralelos. en estos se incluyen el Cuadrado, Rectángulo, Rombo y Romboide.
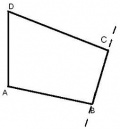
Trapecios: Tienen un solo par de lados paralelos. Dentro de ellos está el isósceles y el escaleno.
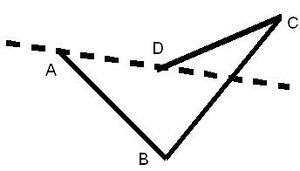
Trapezoides: No tienen ningún lado paralelo a su lado opuesto.
Propiedades
- La suma de los cuatro ángulos interiores equivale a cuatro rectos.
- Tiene dos diagonales en total, y desde un vértice se puede trazar solo una.
- Las diagonales se cortan en un punto interior del trapecio.
Véase también
Fuentes
- Microsoft ® Encarta ® 2007. © 1993--2006 Microsoft Corporation. Reservados todos los derechos.
- Miyares Arturo y Jose M Escalona. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974.