Diferencia entre revisiones de «Integral definida»
m (Corrigiendo errores y sustituyendo las imágenes que no se muestran) |
|||
| Línea 1: | Línea 1: | ||
{{Definición | {{Definición | ||
|nombre=Integral definida | |nombre=Integral definida | ||
| − | |imagen= | + | |imagen=Barrow_area.png |
|tamaño= | |tamaño= | ||
| − | |concepto= | + | |concepto= La '''integral definida''' de ''f(x)'' en el intervalo ''[a,b]'' es igual al área limitada entre la gráfica de ''f(x)'', el eje de abscisas, y las rectas verticales ''x = a'' y ''x = b'' |
}} | }} | ||
<div align="justify"> | <div align="justify"> | ||
| Línea 11: | Línea 11: | ||
La integral definida es uno de los conceptos fundamentales del [[Análisis Matemático|Análisis Matemático]]. | La integral definida es uno de los conceptos fundamentales del [[Análisis Matemático|Análisis Matemático]]. | ||
| − | + | La integral definida de ''f(x)'' en el intervalo ''[a,b]'' es igual al área limitada entre la gráfica de ''f(x)'', el eje de abscisas, y las rectas verticales ''x = a'' y ''x = b'' (bajo la hipótesis de que la función ''f'' es positiva). Esta integral se representa por: | |
| + | <center>[[Image:Integral_f.png]]</center> | ||
| − | + | '''a''' es límite inferior de la integración y '''b''' es límite superior de la integración. | |
| − | '' | + | Si la función ''F'' es una [[función primitiva]] de ''f'' en el intervalo [a,b], por la [[Regla de Barrow]] se tiene que: |
| − | + | <center>[[Image: Regla_Barrow.png]]</center> | |
| − | '''b | ||
== Propiedades == | == Propiedades == | ||
| Línea 23: | Línea 23: | ||
1. El valor de la integral definida cambia de signo si se permutan los límites de integración. | 1. El valor de la integral definida cambia de signo si se permutan los límites de integración. | ||
| − | [[Image: | + | <center>[[Image:Integral_neg.png]]</center> |
2. Si los límites que integración coinciden, la integral definida vale cero. | 2. Si los límites que integración coinciden, la integral definida vale cero. | ||
| − | [[Image: | + | <center>[[Image:Integral_cero.png]]</center> |
3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b]. | 3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b]. | ||
| − | [[Image:PropIntegdef3.gif]] | + | |
| + | <center>[[Image:PropIntegdef3.gif]]</center> | ||
4. La integral definida de una suma de funciones es igual a la suma de integrales· | 4. La integral definida de una suma de funciones es igual a la suma de integrales· | ||
| − | [[Image: | + | <center>[[Image:Integral_suma.png]]</center> |
5. La integral del producto de una constante por una función es igual a la constante por la integral de la función. | 5. La integral del producto de una constante por una función es igual a la constante por la integral de la función. | ||
| − | [[Image:PropIntegdef5.gif]] | + | <center>[[Image:PropIntegdef5.gif]]</center> |
== Ejemplo == | == Ejemplo == | ||
| − | [[Image:Integral_como_Area_DEBAJO_de_una_Curva.JPG]] | + | <center>[[Image:Integral_como_Area_DEBAJO_de_una_Curva.JPG]]</center> |
== Aplicaciones == | == Aplicaciones == | ||
| Línea 50: | Línea 51: | ||
* [[Integración_numérica|Integración numérica]] | * [[Integración_numérica|Integración numérica]] | ||
| − | |||
* [[Integral Indefinida|IIntegral Indefinida]] | * [[Integral Indefinida|IIntegral Indefinida]] | ||
| − | |||
* [[Integración_por_el_método_cambio_de_variable|Integración por Cambio de variable]] | * [[Integración_por_el_método_cambio_de_variable|Integración por Cambio de variable]] | ||
| − | |||
* [[Integración por parte|Integración por parte]] | * [[Integración por parte|Integración por parte]] | ||
| − | |||
* [[Integrales_de_funciones_trigonométricas|funciones trigonométricas]]. | * [[Integrales_de_funciones_trigonométricas|funciones trigonométricas]]. | ||
| − | |||
* [[Integración de funciones racionales|Integración de funciones racionales]]. | * [[Integración de funciones racionales|Integración de funciones racionales]]. | ||
| − | |||
* [[Derivada_de_una_función|Derivada de una función]] | * [[Derivada_de_una_función|Derivada de una función]] | ||
== Fuentes == | == Fuentes == | ||
| + | * [https://www.matesfacil.com/matematicos/Barrow/Isaac-Barrow-primer-segundo-teorema-fundamental-calculo-regla-biografia.html Interpretación de la intgral definida] | ||
* Integral definida [citado 2011 agosto, 10]; Disponible en:http://www.vitutor.net/1/integral_definida.html | * Integral definida [citado 2011 agosto, 10]; Disponible en:http://www.vitutor.net/1/integral_definida.html | ||
| − | |||
* Integrales Definidas [citado 2011 agosto, 10]; Disponible en:http://es.wikipedia.org/wiki/Integraci%C3%B3n | * Integrales Definidas [citado 2011 agosto, 10]; Disponible en:http://es.wikipedia.org/wiki/Integraci%C3%B3n | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión del 12:41 21 ene 2017
| ||||||
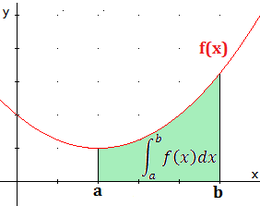
Integral definida. Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.
Definición
La integral definida es uno de los conceptos fundamentales del Análisis Matemático.
La integral definida de f(x) en el intervalo [a,b] es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b (bajo la hipótesis de que la función f es positiva). Esta integral se representa por:
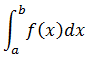
a es límite inferior de la integración y b es límite superior de la integración.
Si la función F es una función primitiva de f en el intervalo [a,b], por la Regla de Barrow se tiene que:
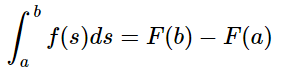
Propiedades
1. El valor de la integral definida cambia de signo si se permutan los límites de integración.
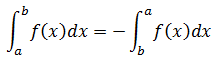
2. Si los límites que integración coinciden, la integral definida vale cero.
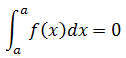
3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].
4. La integral definida de una suma de funciones es igual a la suma de integrales·
5. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
Ejemplo
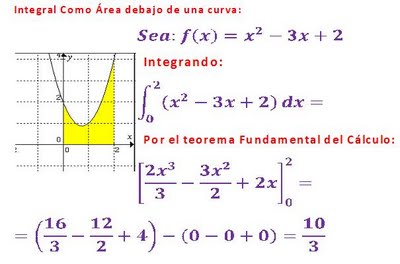
Aplicaciones
El concepto de integral tuvo su origen histórico en la necesidad de resolver problemas concretos como: cálculo de área limitada por dos curvas, longitudes de arcos, volúmenes, trabajo, velocidad, momentos de inercia, etc.; todos estos cálculos se pueden realizar mediante la integral definida.
Véase también
- Integración numérica
- IIntegral Indefinida
- Integración por Cambio de variable
- Integración por parte
- funciones trigonométricas.
- Integración de funciones racionales.
- Derivada de una función
Fuentes
- Interpretación de la intgral definida
- Integral definida [citado 2011 agosto, 10]; Disponible en:http://www.vitutor.net/1/integral_definida.html
- Integrales Definidas [citado 2011 agosto, 10]; Disponible en:http://es.wikipedia.org/wiki/Integraci%C3%B3n