Analisis discriminante en R

Análisis discriminante en R

Análisis discriminante en R: Es un método estadístico que permite clasificar n individuos en m grupos previamente definidos.

Introducción

El análisis de discriminante es una técnica estadística que identifica las variables que permiten diferenciar a los grupos y cuántas de estas variables son necesarias para alcanzar la mejor clasificación posible. Otro de los objetivo de éste análisis es encontrar la combinación lineal de las variables independientes que mejor permiten diferenciar a los grupos. Se trata de una técnica de análisis multivariante que es capaz de aprovechar las relaciones existentes entre una gran cantidad de variables independientes para maximizar la capacidad de discriminación. Es uno de los métodos más sencillo y conocido de clasificación, fue propuesta por Fisher (1936); este enfoque se denomina Análisis Discriminante Lineal (LDA) y básicamente divide el espacio muestral en subespacios mediante hiperplanos que permiten separar lo mejor posible los grupos en estudio. Los supuestos para la utilización de Análisis Discriminante Lineal(LDA) son: normalidad multivariada e igualdad de matrices de covarianzas entre los grupos. El objetivo esencial del análisis discriminante es utilizar los valores previamente conocidos de las variables independientes para predecir en qué categoría de la variable dependiente corresponde. Es decir, asignar nuevos individuos al grupo que mejor corresponde en una clasificación ya establecida, construida a partir de individuos distintos.
El análisis discriminante es la prueba estadística apropiada para seleccionar qué variables independientes o predictivas permiten diferenciar grupos y cuántas de estas variables son necesarias para alcanzar la mejor clasificación posible.

Procedimiento

La pertenencia de los grupos, conocida de antemano, se utiliza como variable dependiente (una variable categórica con tantos valores discretos como grupos). Las variables en las que suponemos se diferencian los grupos se utilizan como variables independientes o variables de clasificación (variables discriminantes).

Aplicación de la prueba

Antes de la utilización de cualquier prueba estadística se debe comprobar el cumplimiento de los supuestos básicos de aplicación. En el caso que nos ocupa se pueden resumir en dos: (i) las variables independientes o predictivas deben seguir una distribución normal multivariante y (ii) las matrices de covarianzas deben ser iguales en todos los grupos.
Aunque el análisis discriminante es considerado una técnica robusta que no se ve gravemente afectada si alguno de los supuestos anteriores no se cumple, En referencia al tipo de variables que deben utilizarse, la variable dependiente debe ser cualitativa (nominal u ordinal) y tener como mínimo dos grupos definidos que sean mutuamente excluyentes y exhaustivos, bien desde el punto de vista de su naturaleza categórica, bien desde su naturaleza dicotómica. No es imprescindible que el volumen de casos sea similar en cada grupo. Las variables independientes utilizadas para el análisis deben ser de intervalo o de razón, y seguir una distribución normal.
Primero e indispensable para ejecutar la función lda (linear discriminant analysis): cargar la librería MASS.
library (MASS)
Ejemplo
library(MASS) # Carga la librería que contiene a la función lda()
data(iris) # Carga los datos de la base de datos iris
datos <- data.frame(iris[,1:4],clase=as.vector(iris[,5]))
especies <- iris[,5] # La columna cinco se refiere a las especies
iris.lda <- lda(clase~.,datos)
iris.lda
Call:
lda(clase ~ ., data = datos)
Prior probabilities of groups:
setosa versicolor virginica
0.3333333 0.3333333 0.3333333
Group means:
Sepal.Length Sepal.Width Petal.Length Petal.Width

setosa	5.006	3.428	1.462	0.246
versicolor	5.936	2.770	4.260	1.326
virginica	6.588	2.974	5.552	2.026

Coefficients of linear discriminants: LD1 LD2
Sepal.Length 0.8293776 0.02410215
Sepal.Width 1.5344731 2.16452123
Petal.Length -2.2012117 -0.93192121
Petal.Width -2.8104603 2.83918785
Proportion of trace:
LD1 LD2
0.9912 0.0088

LD1 y LD2 son los coeficientes de la función discriminante que permite diferenciar a las especies. Como hay 3 especies, aparecen dos funciones discriminantes.

predict(iris.lda,iris[1:4, ])$class #Para clasificar las observaciones

[1] setosa setosa setosa setosa
Levels: setosa versicolor virginica

Tabla <- table(iris[,5],predict(iris.lda,iris[,1:4])$class)

setosa	50	0	0
versicolor	0	48	2
virginica	0	1	49

> z$counts # Este es el número total de observaciones por grupo
c s v
25 25 25
Estos son el número total de individuos asignados a cada especie en la muestra de adiestramiento.
z$svd
[1] 35.776092 3.242579
Poder discriminante de cada función

z$N#The number of observations used.
[1] 75

(pred.class<-predict(z)$class) # Para clasificar las observaciones

[1] s c c s c s v v v c v v s v s v v v c v c v c s c c s c v c s v s v c s s v v s v
[42] c s c v v v s s c s v v c c s v c c s v s s s s s s v s c c s c v v
Levels: c s v

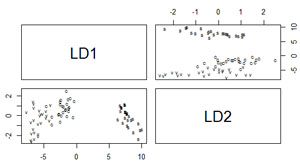
Visualización

Gráfico en el que se observan los grupos

Plot(z)

Pairs(z)

Tras la aplicación del análisis de discriminante podremos:

• Evaluar la exactitud de la clasificación en una tabla cruzada en la que se compara la pertenencia real de los individuos a un grupo con el pronóstico de pertenencia.
  
• Identificar qué variables independientes tienen mayor poder de discriminación y de predicción en la clasificación de sujetos.
  
• Obtener una ecuación denominada ‘función discriminante’ que exprese la combinación lineal de las variables predictivas (denominadas variables canónicas) y permita construir una regla de decisión que asigne un objeto nuevo a uno de los grupos prefijados con un cierto grado de riesgo.

Fuentes

• Barajas, F.H., Morales, J.C.C., 2009. Comparación entre tres técnicas de clasificación. Rev. Colomb. Estad. 32 (2), 247– 265.
• Fisher, R.A., 1936. The use of multiple measurements in taxonomic problems. Ann. Eugen. 7, 179–188.
• Fonseca, M.T., Silvente, V.B., 2013. Análisis Discriminante mediante SPSS. REIRE Rev. D’Innovació Recer. En Educ. 6 (2), 150–166.
• Ripley, B., Venables, B., Bates, D.M., Hornik, K., Gebhardt, A., Firth, D., Ripley, B., 2015. Support Functions and Datasets for Venables and Ripley’s MASS. Package “MASS” [WWW Document]. URL http://cran.us.r-project.org/web/packages/MASS/MASS.pdf. Fecha de revisión: 23/12/2015