Curvatura del espacio-tiempo
| ||||||
Curvatura del espacio. La curvatura del espacio-tiempo es la propiedad del espacio-tiempo en la que las leyes familiares de la geometría no son aplicables en regiones donde los campos gravitatorios son intensos. La relatividad general de Einstein, nos explica y demuestra que el espacio-tiempo está íntimamente relacionado con la distribución de materia en el universo, y nos dice que el espacio se curva en presencia de masas considerables como planetas, estrellas o galaxias (entre otros).
Reseña histórica
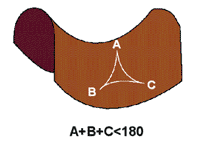
La idea de que el espacio y el tiempo pueden sufrir torsiones o curvarse, es bastante reciente. Durante más de dos mil años, los axiomas de la geometría Euclídea fueron considerados verdades evidentes. Como todos aquellos que se han visto forzados a estudiar geometría Euclídea en el colegio recuerdan, una de las consecuencias de estos axiomas es, que los ángulos de un triángulo, sumados en conjunto, dan como resultado 180 grados. Sin embargo, durante el último siglo, la gente comenzó a darse cuenta de que existían otras formas posibles de geometría, en la que los ángulos de un triángulo, no necesariamente suman 180 grados
Si dibujamos un triángulo con una superficie en forma de silla de montar, descubriremos que la suma de sus ángulos da un resultado menor a 180 grados.
En 1854 el alemán George Friedrich Riemann, desarrolló un modo para describir espacios curvos, esta permaneció como una parte incompleta de las matemáticas durante 60 años. Podía describir espacios curvos que existiesen en el abstracto, pero no había razones por las que creer que el espacio físico en el que vivimos pudiese ser curvo. Esa idea llegó solo en 1915, cuando Einstein presentó la Teoría General de la Relatividad.
Además del espacio plano o euclídeo, podemos construir otros espacios de curvatura constante como: El espacio abierto hiperbólico de Bolyai-Lobachevski en el que existe, no una sino infinitas rectas paralelas a una recta dada que pasen por un punto exterior prefijado. El espacio cerrado elíptico de Riemann en el que no existe ninguna recta paralela exterior a otra dada que no se intersequen.
El campo gravitatorio solar viene dado de manera aproximada por la métrica de Schwarzschild, que a distancias muy grandes se aproxima a geometría plana del espacio de Minkowski. La figura muestra aproximadamente el plano de la eclíptica del sistema solar modelizado mediante la métrica de Schwarzschild, una órbita planetaria es una curva cuasi-elíptica alrededor del centro de dicha eclíptica.
Una representación del paraboloide de Flamm, cuya curvatura geométrica coincide con la del plano de la eclíptica o ecuatorial de una estrella esféricamente simétrica.
Midiendo la curvatura del espacio
Gauss había mostrado que pueden existir otras geometrías no-euclídeas, lo cual sugería que la geometría real del espacio no tenía por qué ser euclídea. Si la geometría del espacio no fuera euclídea habría ciertas consecuencias medibles, por ejemplo, si un físico pone una marca, y un cartógrafo permanece a una cierta distancia y se mide su longitud por triangulación basada en la geometría euclídea, entonces no está garantizado que sea dada la misma respuesta si el físico porta la marca consigo y mide su longitud directamente.
Por supuesto, para una marca no podría medirse en la práctica la diferencia entre las dos medidas, pero existen medidas equivalentes que deben detectar la geometría no euclidiana del espacio-tiempo directamente, por ejemplo el experimento de Pound-Rebka (1959) detectó el cambio en la longitud de onda de la luz de una fuente de cobalto surgiendo por 22.5 metros contra la gravedad en un local del Laboratorio de Física Jefferson en la Universidad de Harvard, y la cadencia de un reloj atómico en un satélite GPS alrededor de la Tierra tiene que ser corregida por efecto de la gravedad.
Fuente
- «Curvatura del espacio-tiempo», artículo publicado en el sitio web Biblioteca Digital ILCE.edu. Consultado el 8 de diciembre del 2013.
- «Curvatura del espacio-tiempo», artículo publicado en el sitio web Wikipedia. Consultado el 8 de diciembre del 2013.
- «Curvatura del espacio-tiempo», artículo publicado en el sitio web El Universo (España) Consultado el 8 de diciembre del 2013.