Funciones logarítmicas
≠≠
Funciones logarítmicas. Funciones inversas a las funciones exponenciales.
Sumario
Definición
El logaritmo de un número y es el exponente al cual hay que elevar la base b para obtener a y. Esto es, si b es un número positivo estricto y b es diferente de 1, entonces:
logb y = x si y sólo si y = bx.
Nota: La notación logb y = x se lee “el logaritmo de y en la base b es x”.
Función logarítmica
Sea a>0, (a ≠ 1), un número real. Se define la función logarítmica de base a como:
f: R*+ → R
x → R
Historia
Históricamente, los exponentes fueron introducidos en matemáticas para dar un método corto que indicara el producto de varios factores semejantes, y, con este propósito, solo se consideraron inicialmente exponentes naturales.
La noción de progresión geométrica no es nueva en Matemática. Existe evidencia que muestra que los egipcios y babilonios manejaban este concepto, y desde luego también los griegos. En Los elementos de Euclides aparece un enunciado que establece la igualdad
am+n = aman
para n y m enteros positivos.
Ya en la Edad Media, N. Oresme (francés, s. XIV) vuelve a hallar esta regla, hablando de exponentes racionales, y estableciendo otras identidades como
(ab)1/n = a1/nb1/n
Sus ideas, muy avanzadas para la época, no fueron entendidas, y un siglo después N. Choquet las retoma, introduciendo además exponentes enteros no positivos. En esta época se consolida la función exponencial (no conocida como tal) como isomorfismo entre los números reales (no conocidos como tales). En el siglo XVI, el matemático alemán Stifel completó el trabajo, introduciendo exponentes racionales arbitrarios, y el paso a exponentes reales fue realizado por J. Neper2.1 (o Napier) y J. Bürgi entre 1614 y 1620, de manera intuitiva. Desde entonces, y hasta mediados del siglo XIX, se admitió esta manera intuitiva de pasar a exponentes reales, al no disponerse de una teoría sólida de números reales que permitiera hacerlo más rigurosamente.
Aunque hoy en día se enseñan a veces como un tema aislado, lo cierto es que los logaritmos (y por ende, las potencias) aparecieron como una herramienta de cálculo. En efecto, al parecer ya Arquímedes utilizaba la idea de reducir la multiplicación de dos números (potencias de 2, por ejemplo), por medio de la suma de sus logaritmos. Pero el verdadero auge de los logaritmos, como herramienta de cálculo, sobre todo en navegación, finanzas y cálculos astronómicos, comienza en el siglo XVI con Stifel, y se consolida a inicios del siglo XVII con Neper y Bürgi, y posteriormente con la construcción de las primeras tablas de logaritmos en base 10, realizadas por H. Briggs (1631).
Las tablas de logaritmos se fueron perfeccionando a través de los años, y fueron utilizadas en los cálculos y en la enseñanza hasta hace relativamente poco tiempo. La era de la computación fue haciendo que las tablas fueran más fáciles de elaborar, pero también las hizo innecesarias, pues ahora es más simple presionar un par de teclas en la calculadora, que buscar mantizas y características.
Con el nacimiento del Cálculo Infinitesimal, las funciones exponencial y logarítmica comienzan a tener importancia desde un punto de vista teórico, al comenzar a ser estudiadas sus propiedades diferenciales. La importancia teórica de estas funciones ha invadido casi la totalidad de las áreas de la Matemática, sobre todo aquellas en que las nociones del cálculo diferencial e integral están presentes. Por otro lado, su importancia desde un punto de vista aplicado va mucho más allá de su uso en los cálculos numéricos. Estas funciones ya no se enseñan más como simple herramienta de cálculo numérico, sino como base de modelos sofisticados y poderosa herramienta teórica en diferentes áreas del quehacer científico.
Propiedades
Las funciones logarítmicas de base a cumplen las siguientes propiedades:
- Son continuas en R*+. Esto significa que si x se acerca a x0, entonces loga(x) se acerca a loga(x0)
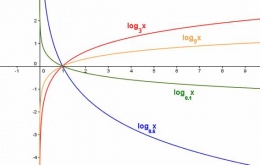
- Pasan por (1;0) y (a;1); en visión geométrica el logaritmo de 1 es siempre 0, y el logaritmo de la base a es 1. Además si x se acerca a 0 por la derecha, sus logarimos tienden a -∞.
- Si a>1 son crecientes y si 0<a<1 son decrecientes. Su crecimiento es menor que el de las funciones raíz de cualquier índice
- La función logaritmica y la exponencial de la misma base son funciones inversas y por tanto sus gráficas son simétricas respecto de la recta y=x
Función logarítmica como inversa de la exponencial
Las funciones y = bx y y = logb(x)para b>0 y b diferente de uno son funciones inversas. Así que la gráfica de y = logb(x) es una reflexión sobre la recta y = x de la gráfica de y = bx. La gráfica de y = bx tiene como asíntota horizontal al eje de x mientras que la gráfica de y = logb(x) tiene al eje de y como asíntota vertical.
Ejemplos de representación gráfica de funciones logarítmicas
a) y = log2(x)
| x | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 |
|---|---|---|---|---|---|---|---|
| f(x) | (-3) | (-2) | (-1) | 0 | 1 | 2 | 3 |
Representación gráfica
b)y = log1/2(x)
| x | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 |
|---|---|---|---|---|---|---|---|
| f(x) | 3 | 2 | 1 | 0 | (-1) | (-2) | (-3) |
Representación gráfica
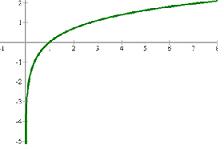
c) y=ln(x)
| x | 0,1 | 0,5 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| f(x) | (-2,3) | (-0,7) | (0) | 0,7 | 1,1 | 1.4 | 1,6 |
Representación gráfica
Fuentes
- Funciones logarítmicas. Disponible en "www.vitutor.com". Consultado el 30 de septiembre 2011
- Exponenciales. Disponible en "www.docencia.udea.edu.co". Consultado el 30 de septiembre 2011
- Datos. Disponible en "www.bc.inter.edu". Consultado el 30 de septiembre 2011
- Contenido-Unidad 1. Disponible en "www.unizar.es". Consultado el 30 de septiembre 2011